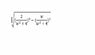- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Learn How to Manipulate a Formula to Find 1/(sqr(w^2+4)) in Simple Steps
- Thread starter greg997
- Start date
In summary, the conversation discusses a formula and attempts to manipulate it to obtain 1/(sqr(w^2+4). The conversation also includes some hints and tips on how to solve the problem.
Physics news on Phys.org
- #2
- 3,105
- 7,670
The two equations are not equal. Just replace w by any value and you'll see that both equations give different answers.
- #3
Mentallic
Homework Helper
- 3,802
- 95
The best you can really get is:
[tex]\frac{\sqrt{4-w^2}}{w^2+4}[/tex]
[tex]\frac{\sqrt{4-w^2}}{w^2+4}[/tex]
Last edited:
- #4
Mentallic
Homework Helper
- 3,802
- 95
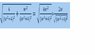
You must have made a typo. The expression should be,
[tex]\sqrt{\left(\frac{2}{w^2+4}\right)^2+\left(\frac{w}{w^2+4}\right)^2}[/tex]
[tex]\sqrt{\left(\frac{2}{w^2+4}\right)^2+\left(\frac{w}{w^2+4}\right)^2}[/tex]
- #5
greg997
- 107
- 2
Mentallic said:You must have made a typo. The expression should be,
[tex]\sqrt{\left(\frac{2}{w^2+4}\right)^2+\left(\frac{w}{w^2+4}\right)^2}[/tex]
Hmm, that's quite possible. Then how to get that solution?
- #6
Mentallic
Homework Helper
- 3,802
- 95
Well I can't just give you the answer, you need to show an attempt at solving the problem first.
But I can give you some hints, you can most certainly find the answer by using a combination of these rules:
[tex]\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}[/tex]
[tex]\sqrt{a^2b}=|a|\sqrt{b}[/tex] (the |a| means the positive of a, but remember that for any real number n, n2 is always positive).
[tex]\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}[/tex]
[tex]\frac{\sqrt{a}}{a}=\frac{1}{\sqrt{a}}[/tex]
Good luck!
But I can give you some hints, you can most certainly find the answer by using a combination of these rules:
[tex]\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}[/tex]
[tex]\sqrt{a^2b}=|a|\sqrt{b}[/tex] (the |a| means the positive of a, but remember that for any real number n, n2 is always positive).
[tex]\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}[/tex]
[tex]\frac{\sqrt{a}}{a}=\frac{1}{\sqrt{a}}[/tex]
Good luck!
- #7
- #8
Cyosis
Homework Helper
- 1,495
- 5
You're adding fractions, but you're multiplying numerators.
- #9
greg997
- 107
- 2
AAA, stupid me:) Thanks
1. How do I approach a simple problem that I can't solve?
The best approach to solving a simple problem is to break it down into smaller, more manageable parts. Start by identifying what is known and what is unknown, then try to find patterns or connections between them. If you are still stuck, try looking at the problem from a different perspective or seeking help from others.
2. Why am I struggling with a seemingly easy problem?
There can be many reasons why a simple problem may be challenging for you. It could be due to a lack of understanding or knowledge in a particular area, lack of focus or attention, or even feeling overwhelmed or stressed. It's essential to identify the root cause of your struggle and address it accordingly.
3. How can I improve my problem-solving skills for simple problems?
Practice, practice, practice! The more you work on simple problems, the better you become at identifying patterns, connections, and potential solutions. It's also helpful to learn different problem-solving techniques and strategies and apply them to different types of problems. Don't be afraid to make mistakes and learn from them.
4. Is there a specific way to approach a simple problem?
There is no one-size-fits-all approach to solving problems. However, some general steps can guide you in the right direction. These include understanding the problem, breaking it down into smaller parts, brainstorming potential solutions, testing and evaluating those solutions, and refining them if necessary. Remember to be flexible and adapt your approach as needed.
5. What resources can I use to help me solve a simple problem?
There are many resources available to help you solve simple problems. These can include textbooks, online tutorials, forums, and even seeking help from a mentor or colleague. It's essential to use reliable sources and ask for help when needed. Remember that collaboration and learning from others can often lead to better solutions than working alone.
Similar threads
-
Precalculus Mathematics Homework Help
- Replies
- 16
- Views
- 977
-
Precalculus Mathematics Homework Help
- Replies
- 11
- Views
- 1K
-
Precalculus Mathematics Homework Help
- Replies
- 8
- Views
- 777
- Replies
- 2
- Views
- 953
-
Precalculus Mathematics Homework Help
- Replies
- 1
- Views
- 526
-
Precalculus Mathematics Homework Help
- Replies
- 8
- Views
- 1K
-
Precalculus Mathematics Homework Help
- Replies
- 19
- Views
- 1K
-
General Math
- Replies
- 3
- Views
- 1K
-
Precalculus Mathematics Homework Help
- Replies
- 2
- Views
- 898
-
Calculus and Beyond Homework Help
- Replies
- 8
- Views
- 1K
Share: