- #1
taureau20
- 9
- 0
Knowing that the torsional spring is of constant K and that the rigid bar is of length L, determine the critical load [TeX]P_{cr}[/TeX] beyond which the column would buckle. See pic for the problem.
[As the spring uncurls, it applies moment [TeX]K \theta[/TeX] to the bar.]
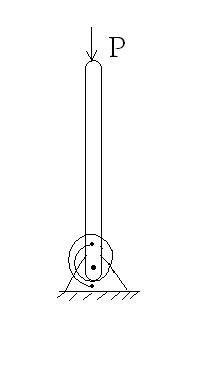
The answer is [tex]P_{cr}=K/L[/tex]
[As the spring uncurls, it applies moment [TeX]K \theta[/TeX] to the bar.]
The answer is [tex]P_{cr}=K/L[/tex]