PotentialE
- 57
- 0
Homework Statement
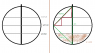
A cylindrical tank of gas with a radius is viewed from the side (so that it looks like a circle, not a rectangle) and has a radius of 1m. Through a hole in the top, a vertical rod is lowered to touch the bottom of the tank. When the rod is removed, the gasoline level in the tank can be read from the mark on the rod. Where on the rod would the mark be if the tank was 3/4 full?
Homework Equations
A = ∏r2
The Attempt at a Solution
I attached a picture (in paint) of my attempts, which mainly consist of some trig, but I can't seem to put it all together