Simple Harmonic Motion and equilibrium of springs

[Mateus Buarque]

The figure below shows a system in equillibrium. The pulley and the springs (both with constants "k") are ideal. The period of oscillation of the mass A is given by:

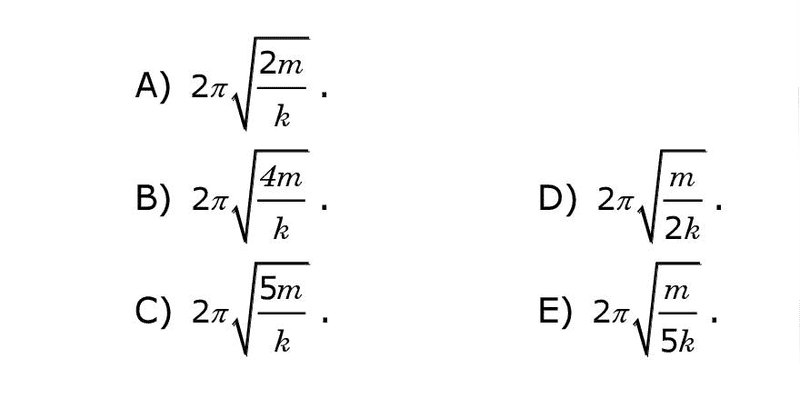
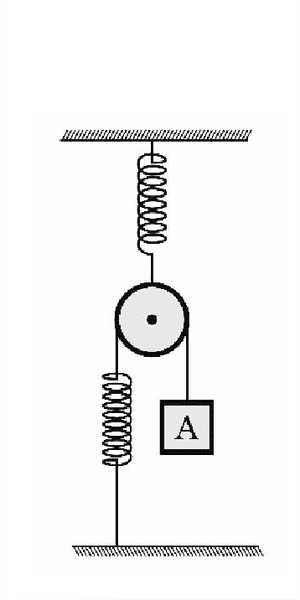
Relevant equations:

F = -kx (SHM)

I tried to do a "force diagram" and set up some geometric relations but it´s not working.

 

[BvU]

Hi,

You can start with discarding the answers that have the wrong dimension.
Your relevant equation needs a few colleagues: at least one with a dimension of time.
Would you know how the period for a simple mass hanging from a spring comes about ?
What is the restoring force for a disturbance from equilibrium in your system ?

Oh, and I notice you haven't been welcomed, so here goes:
Hello Mateus, !

 

[gneill]

I tried to do a "force diagram" and set up some geometric relations but it´s not working.

Please show the details of what you have tried.

 

[Mateus Buarque]

Hi,

You can start with discarding the answers that have the wrong dimension.
Your relevant equation needs a few colleagues: at least one with a dimension of time.
Would you know how the period for a simple mass hanging from a spring comes about ?
What is the restoring force for a disturbance from equilibrium in your system ?

Oh, and I notice you haven't been welcomed, so here goes:
Hello Mateus, !

Thank you but no answer has a wrong dimension, cause they are all in the form of a constant*root(m/k), which is correct!

 

[BvU]

Oops, so that doesn't help. Now how about the 'combined' spring constant ? What is the restoring force if I pull down the mass over a small distance $x$ ?