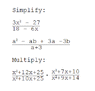Simplifying Fractions and Multiplying Basics - Tips for Easy Math Solutions

[Sanyo]

Hello! I have a major final on Friday and I need to figure out how to do these problems. For the life of me I canot figure out how to simplify those fractions. And to multiple, I was under the impression you factor out first and then cross out. But everything comes out positive?

For the multiplication, it should be x2+12x+35, not 25. sorry

Any help is appreciated!

 

[arildno]

Let's take the first:
\frac{3x^{2}-27}{18-6x}
It is smart to focus on the numerator and denominator separately:
FIRST SIMPLIFICATION:
Numerator: 3x^{2}-27
Note that 3 is common factor, since 27=3*9.
Therefore, you can write:
3x^{2}-27=3*(x^{2}-9)
Denominator: 18-6x
Here, 6 is a common factor, since 18=6*3
Thus, you can write: 18-6x=6*(3-x)

Therefore, we have:
\frac{3x^{2}-27}{18-6x}=\frac{3*(x^{2}-9)}{6*(3-x)}
But, now we can see that because 6=3*2, we have:
\frac{3*(x^{2}-9)}{6*(3-x)}=\frac{3*(x^{2}-9)}{3*2*(3-x)}=\frac{(x^{2}-9)}{2*(3-x)}
We have managed a simplification!

SECOND SIMPLIFICATION:
Numerator:
If you are perceptive, you see that we have: x^{2}-9=(x+3)*(x-3)
Let us write this a bit differently, by extracting a minus sign from the last parenthesis:
x^{2}-9=(x+3)*(x-3)=-(x+3)*(3-x)
But now, we have:
\frac{(x^{2}-9)}{2*(3-x)}=\frac{-(x+3)*(3-x)}{2*(3-x)}=-\frac{(x+3)}{2}
since the factor (3-x) occurs in both numerator and denominator.
Got that?

 

[dextercioby]

Can u factor them...?All of them can be factored & easily simplified.Take the first.What can u do to it...?

Daniel.

 

[Galileo]

In all those problems the idea is to factorize.
Some useful identities will help you spot how to factor certain polynomials immediately:

(a+b)^2=a^2+2ab+b^2
(a-b)^2=a^2-2ab+b^2
(a+b)(a-b)=a^2-b^2

Identifying the right side will help you factor it as the left side. eg: x^2-9=x^2-3^2=(x+3)(x-3).

Also, be careful when simplifying as follows:

\frac{x^2-25}{x-5}=\frac{(x+5)(x-5)}{x-5}=x+5

In the last step I divided top and bottom by x-5, which is not allowed when x=5. So the last step is wrong. Be sure to add x\not=5 or don't simplify further.

 

[arildno]

I would rather say that x isn't allowed to be 5 in the first place..
In my case, Galileo's argument requires that x must be different from 3.

 

[Sanyo]

Thanks! That was stupid, all I had to do was factor out.

But for the multiplication, I'm still unsure.

wouldn't x2+12x+35 = (x+7)(x+5) ?

and x2+10x+25 = (x+5)(x+5)

and for x2+7x+10 = (x+5)(x+2)

and for x2+9x+14= (x+7)(x+2)

 

[The Bob]

\frac{x^2 + 12x + 25}{x^2 + 10x + 25} \times \frac{x^2 + 7x + 10}{x ^2 + 9x + 14} =

\frac{x^4 + 7x^3 + 10x^2 + 12x^3 + 84x^2 + 120x + 25x^2 + 175x + 250}{x^4 + 9x^3 + 14x^2 + 10x^3 + 90x^2 + 140x + 25x^2 + 225x + 350} etc. is one way or you can factorise.

The Bob (2004 ©)

 

[arildno]

Sure, your factoring looks okay to me.

 

[arildno]

\frac{x^2 + 12x + 25}{x^2 + 10x + 25} \times \frac{x^2 + 7x + 10}{x ^2 + 9x + 14} =

\frac{x^4 + 7x^3 + 10x^2 + 12x^3 84x^2 + 120x + 25x^2 + 175x + 250}{x^4 + 9x^3 + 14x^2 + 10x^3 + 90x^2 + 140x + 25x^2 + 225x + 350} etc.

The Bob (2004 ©)

You have a delightfully original conception of SIMPLIFICATION, THe Bob!

 

[The Bob]

You have a delightfully original conception of SIMPLIFICATION, THe Bob!

The original question says multiply. Not a word about simplification.

Sure, your factoring looks okay to me.

It might be ok but if you see the original question the first:

x^2+12x+35 = (x+7)(x+5)

should be x^2 + 12x + 25, hence, the longer way of doing it.

The Bob (2004 ©)

 

[Sanyo]

Should be:

\frac{x^2 + 12x + 35}{x^2 + 10x + 25} \times \frac{x^2 + 7x + 10}{x ^2 + 9x + 14}

and then I thought it was:

\frac{(x+7)(x+5)}{(x+5)(x+5)} \times \frac{(x+5)(x+2)}{(x+7)(x+2)}

Would they all cancel out making it 1?

 

[arildno]

That seems correct.

 

[learningphysics]

Should be:

\frac{x^2 + 12x + 35}{x^2 + 10x + 25} \times \frac{x^2 + 7x + 10}{x ^2 + 9x + 14}

and then I thought it was:

\frac{(x+7)(x+5)}{(x+5)(x+5)} \times \frac{(x+5)(x+2)}{(x+7)(x+2)}

Would they all cancel out making it 1?

Exactly! Well done.

EDIT: Follow Galileo's advice and write that x cannot equal -5,-7 or -2.

 

[The Bob]

Should be:

\frac{x^2 + 12x + 35}{x^2 + 10x + 25} \times \frac{x^2 + 7x + 10}{x ^2 + 9x + 14}

Now that this information has come out, I would like to apologise to arildno for an offence I may have caused. With the information given I did not see a simpler way without the quadratic equation. Please accept my apologise.

The Bob (2004 ©)

 

[arildno]

Now that this information has come out, I would like to apologise to arildno for an offence I may have caused. With the information given I did not see a simpler way without the quadratic equation. Please accept my apologise.

The Bob (2004 ©)

None needed; I was able to sleep unperturbed last night, and that's the important thing, isn't it?

 

[The Bob]

None needed; I was able to sleep unperturbed last night, and that's the important thing, isn't it?

Yeap. It is.

The Bob (2004 ©)