Johnnnnnnnn
- 8
- 0
Hi guys! I am currently learning about fluid dynamics, and I am stuck on a certain equation derivation. It's about sinking motion which considers only gravity force, buoyant force, and viscous resistance. The link attached has the details.
http://hyperphysics.phy-astr.gsu.edu/hbase/lindrg.html#c2
The problem I have is how the equation for velocity was found. I understand that Fnet = mg - pVg - bv, which is basically net force = weight - buoyant force - viscous resistance, but I don't get how the velocity (equation below) was derived in terms of time, terminal velocity (Vt), and initial velocity (V0).
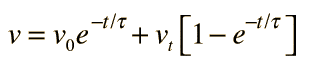
Is there a mathematical proof for this? Or was the equation created based on trial and error? If you could, could you also please explain how the equation for distance (image below) was also obtained? Thanks!
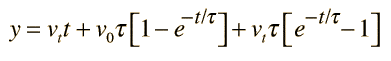 .
.
http://hyperphysics.phy-astr.gsu.edu/hbase/lindrg.html#c2
The problem I have is how the equation for velocity was found. I understand that Fnet = mg - pVg - bv, which is basically net force = weight - buoyant force - viscous resistance, but I don't get how the velocity (equation below) was derived in terms of time, terminal velocity (Vt), and initial velocity (V0).
Is there a mathematical proof for this? Or was the equation created based on trial and error? If you could, could you also please explain how the equation for distance (image below) was also obtained? Thanks!