B Sinusoidal wave function of t and x

[Ennio]

TL;DR Summary

Starting from the domain of t, is it possible to express the sinef function under the domain of movement?

Greetings,

is it possible to characterize a sinusoidal wave in the domain of time and then pass into the domain of movement along x direction?
I start with: a is the amplitude of the sine function and ω is the angular velocity. t is the time. I can express the angular velocity in funct. of the frequency n. In turn, n is velocity of the wave valong x divided its wavelength. Now, 2 pi over lambda is the wave number k and vt is the movement along x.
Does my derivation make sense to you?

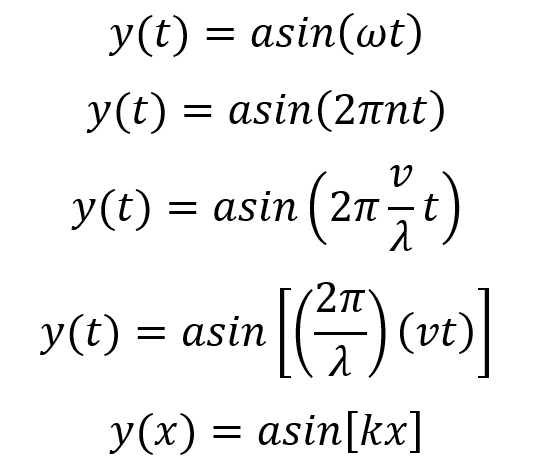
E.

 

[robphy]

Are you trying to describe the disturbance $y$ from equilibrium

• for a single particle located at $x=X_P$ in a medium as time evolves? $y(X_P,t)$
• for the shape of a string (made up of a string of particles) at a certain time $T_0$ ? $y(x,t=T_0)$
• for the shape of a string (made up of a string of particles) as time evolves? $y(x,t)$

 

[Ennio]

Are you trying to describe the disturbance $y$ from equilibrium

• for a single particle located at $x=X_P$ in a medium as time evolves? $y(X_P,t)$
• for the shape of a string (made up of a string of particles) at a certain time $T_0$ ? $y(x,t=T_0)$
• for the shape of a string (made up of a string of particles) as time evolves? $y(x,t)$

not exactly a disturbance from equilibrium but rather the description of the sine wave evolution i nthe two domains.