ankyk91
- 3
- 0
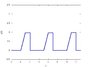
I sketched the signal for y(t) and my answer is shown pic1.jpg
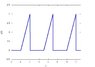
but apparently it's wrong and the right answer from the tutorial answers is shown in pic2.jpg. So could someone tell me what I have done wrong. Thanks
Consider the signal
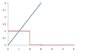
x(t) = r(t) u(2-t)
where r(t) is the ramp function and u(t) is the step function.
The signal y(t) is formed as the periodic extension of x(t) with period 5
a. Clearly sketch the signal y(t).
but apparently it's wrong and the right answer from the tutorial answers is shown in pic2.jpg. So could someone tell me what I have done wrong. Thanks
Homework Statement
Consider the signal
x(t) = r(t) u(2-t)
where r(t) is the ramp function and u(t) is the step function.
The signal y(t) is formed as the periodic extension of x(t) with period 5
a. Clearly sketch the signal y(t).