Slider crank mechanism mass moment of inertia

[blaster]

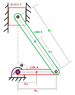
I need help solving a mass moment of inertia for a slider crank mechanism. I've done my best to sketch it in the attachment. This will be used for sizing of a motor.

Homework Statement

Link A has mass Ma and is located Acg distance from its pivot point Z
Link B has mass Mb and is located Bcg distance from its connection to Link A
Block C has mass Mc and has a frictionless retainment vertical of point Z
Link A is at and Angle theta from vertical.
Find the mass moment of inertia about point Z.

Homework Equations

Its been too long

The Attempt at a Solution

Tried using engineering programs to figure it out numerically.

 

[RTW69]

You have three masses, I_tot=m1*r1^2+m2*r2^2+m3*r3^2 where the radius is the distance from z

 

[blaster]

But I want the moment of inertia about z. So the constraints in motion play a part. for example when theta is zero the block mass is not moving much with respect to theta. At 90 degrees the block is moving a lot with respect to theta.

I may have not been clear but the inertia is changing dependent upon theta.

 

[RTW69]

Are you trying to find I_total as a function of theta? If so you can use the law of sines to find the interior angles of the linkage and the vertical distance from block c to z. You need everything in terms of B_tl, theta and A_tl. The distance from B_cg to z can be found using the law of cosines since you found the angle between link B and A using the law of Sines above. Now that you know the distances from the center of mass of each element you can find I_total in terms of theta.