So fustrated and need some desperate help

[HighVoltage]

all,
i am stuck on this problem. physics has not been good to me this semester. its like "in one ear out the other"

this is the problem:

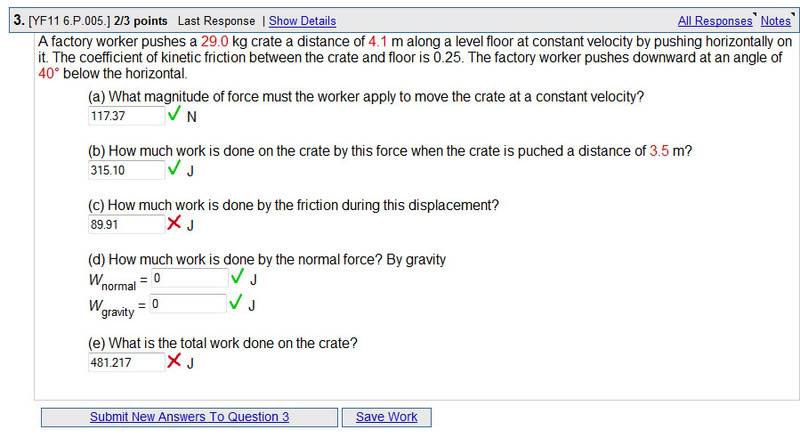
i can't get c or d.

for c i tried .25(29*9.8+117.37*sine(40)) that wasnt right

for d i tried 117.37*4.1 and that wasnt right

please help me.

 

[learningphysics]

For part c), you forgot to multiply by the distance... also the work by friction is negative...

Think about this... the crate is moved at constant velocity... so what is the net work done on it by all forces? (what does the work energy theorem say?)

 

[m2003]

I understand that you are feeling frustrated and in need of help with a physics problem. It can be challenging to grasp certain concepts in science, but please do not give up. I can offer some guidance to help you understand and solve this problem.

First, let's break down the problem into smaller parts. For part c, it seems like you are trying to calculate the force using the formula F=ma. However, the formula for force in this case should be F=mg+ma, where "m" is the mass, "g" is the acceleration due to gravity (9.8 m/s^2), and "a" is the acceleration in the direction of the force. The angle of 40 degrees is not needed in this formula. So, your calculation should be 0.25(29*9.8)+117.37= 120.6075 N.

For part d, you are trying to calculate the weight of the object, which is the force due to gravity acting on the object. So the correct formula is W=mg, where "m" is the mass and "g" is the acceleration due to gravity. So your calculation should be 117.37*9.8= 1150.426 N.

I hope this helps you understand the problem better and solve it correctly. Remember to always check your units and formulas to ensure accuracy. Keep practicing and seeking help when needed, and you will improve in physics. Best of luck!