I'm going to start from the beginning now the make sure its all allright
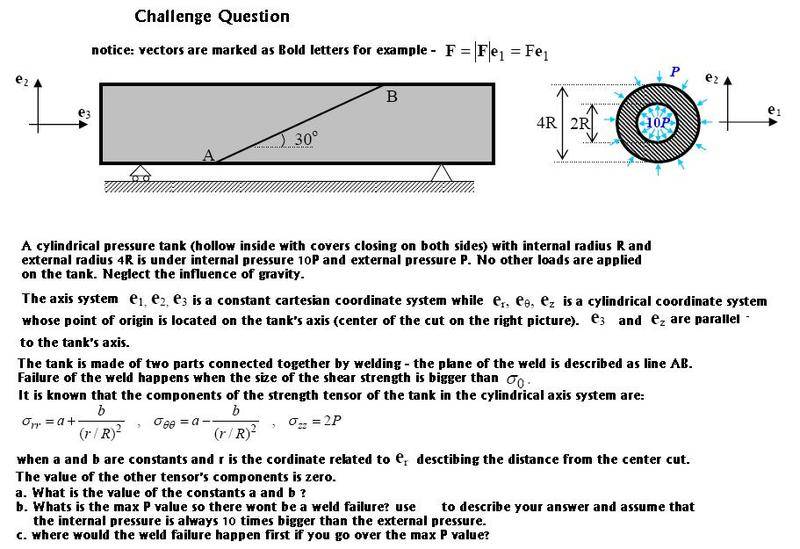
1. finding the constants:
\sigma_{rr}(r=R)=a+b=-10P, \sigma_{rr}(r=2R)=4a+b=-4P
we comapre these exprassions to \ -10P,-P and not to \+10P,-P because the sign (-) says that the tank is under compression from the inner and outer surface?
This gives us a=2P, b=-12P
2.a The stress tensor in cylindrical coordinates (r,\theta,z):
\sigma_{(r,\theta,z)}=\begin{pmatrix}<br />
2P-\frac{12P}{(r/R)^{2}} & 0 & 0 \\<br />
0 & 2P+\frac{12P}{(r/R)^{2}} & 0 \\<br />
0 & 0 & 2P \end{pmatrix}
2.b Switching from cylindrical coordinates (r,\theta,z) to cartesian (x,y,z), z remains the same:
R - transform matrix from cylinder to cartesian
\sigma_{(x,y,z)}=R^{T}\cdot \sigma_{(r,\theta,z)}\cdot R,
R=\begin{pmatrix}cos(\theta) & -sin(\theta) & 0 \\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 &1\end{pmatrix}
\sigma_{(x,y,z)}=\begin{pmatrix}\sigma_{xx} & \sigma_{xy} & \sigma_{xz} \\ \sigma_{yx} & \sigma_{yy} & \sigma_{yz} \\ \sigma_{zx} & \sigma_{zy} & \sigma_{zz}\end{pmatrix}=\begin{pmatrix}cos(\theta) & sin(\theta) & 0 \\ -sin(\theta) & cos(\theta) & 0 \\ 0 & 0 &1\end{pmatrix}\begin{pmatrix}\sigma_{rr} & \sigma_{r\theta} & \sigma_{rz} \\ \sigma_{\theta r} & \sigma_{\theta\theta} & \sigma_{\theta z} \\ \sigma_{zr} & \sigma_{z\theta} & \sigma_{zz}\end{pmatrix}\begin{pmatrix}cos(\theta) & -sin(\theta) & 0 \\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 &1\end{pmatrix}=
=\begin{pmatrix}cos(\theta) & sin(\theta) & 0 \\ -sin(\theta) & cos(\theta) & 0 \\ 0 & 0 &1\end{pmatrix}\begin{pmatrix}2P-\frac{12P}{(r/R)^{2}} & 0 & 0 \\ 0 & 2P+\frac{12P}{(r/R)^{2}} & 0 \\ 0 & 0 & 2P \end{pmatrix}\begin{pmatrix}cos(\theta) & -sin(\theta) & 0 \\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 &1\end{pmatrix}
2.c Transforming the cartesian coordinate system by 30 degrees - \sigma':
A - transformation matrix in the cartesian coordinate system by 30degrees
\sigma'_{(x,y,z)}=A^{T}\cdot \sigma_{(x,y,z)}\cdot A=A^{T}R^{T}\sigma_{(r,\theta,z)}RA,
A=\begin{pmatrix}1 & 0 & 0 \\0 & cos(60) & sin(60) \\0 & -sin(60) & cos(60) \end{pmatrix}
The stress wall on AB is then:
\sigma'_{(x,y,z)}= \begin{pmatrix}<br />
1 & 0 & 0 \\<br />
0 & cos(60) & -sin(60) \\<br />
0 & sin(60) & cos(60) \end{pmatrix} \begin{pmatrix}cos(\theta) & sin(\theta) & 0 \\ -sin(\theta) & cos(\theta) & 0 \\ 0 & 0 &1\end{pmatrix}\begin{pmatrix}2P-\frac{12P}{(r/R)^{2}} & 0 & 0 \\ 0 & 2P+\frac{12P}{(r/R)^{2}} & 0 \\ 0 & 0 & 2P \end{pmatrix}\begin{pmatrix}cos(\theta) & -sin(\theta) & 0 \\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 &1\end{pmatrix} \begin{pmatrix}<br />
1 & 0 & 0 \\<br />
0 & cos(60) & sin(60) \\<br />
0 & -sin(60) & cos(60) \end{pmatrix}
I'm waiting with the multiplication to see if you think I wrote it correctly this far, if so I can find the shear stress on AB by using the following connection:
\sigma_{ns}=s_i \cdot \sigma_{ij} \cdot n_i when \hat{s} and \hat{n} are unit vectors pointing in the direction of the shear and normal stress.