Solution related to certain condition in quadratic equation

[songoku]

Homework Statement

For a constant k, consider the function f(x) = x² + kx + k² - 2k - 4
Find the range of k for which f(x) = 0 has one solution between 0 and 1 and the other solution between 1 and 2

Homework Equations

quadratic formula
discriminant

The Attempt at a Solution

x² + kx + k² - 2k - 4 = 0

Using quadratic formula:
x=\frac{-k±\sqrt{-3k^2+8k+16}}{2}

Then I set:
0 < \frac{-k-\sqrt{-3k^2+8k+16}}{2} < 1 and 1 < \frac{-k+\sqrt{-3k^2+8k+16}}{2} < 2

Am I on the right track? I think solving that inequality will take a lot of work... Is there other method?

Thanks

 

[Infinitum]

Your method is correct, though very tedious. Another thing you can try is see how the graph of the quadratic is.

Meaning, the curve f(x) intersects x axis(has 2 roots), what condition does this give you for the discriminant?
Then, for a root to be in (0,1) and the other to be in (1,2) what should the nature of product of f(0) and f(2) be? Will this be a necessary -and- sufficient condition?

Drawing a rough graph will help

 

[ehild]

Try to use the relation between coefficients and roots of the quadratic equation.

ehild

 

[Infinitum]

Try to us the relation between coefficients and roots of the quadratic equation.

ehild

This is actually an easier method to understand, than I suggested

 

[songoku]

Try to us the relation between coefficients and roots of the quadratic equation.

ehild

I am not sure what you mean by "relation between coefficients and roots of the quadratic equation". Are you talking about Vieta's formula?

If yes, I don't see how Vieta's formula can form inequality to find range of k...

If no, then I don't what your hint means...

 

[Infinitum]

I am not sure what you mean by "relation between coefficients and roots of the quadratic equation". Are you talking about Vieta's formula?

If yes, I don't see how Vieta's formula can form inequality to find range of k...

If no, then I don't what your hint means...

Yes, the Vieta formula. Consider the roots to be A and B.

A + B = ??

A*B = ??

Hint : you already know the lowest possible value for your roots is in (0,1) and the highest is in (1,2) How can you get an interval of sum of roots and product from this?

 

[ehild]

It was Vieta! I could not remember the name.
One condition comes also from the discriminant -3k²+8k+16. It can not be negative.
So you have three condition for k...

ehild

 

[songoku]

Yes, the Vieta formula. Consider the roots to be A and B.

A + B = ??

A*B = ??

Hint : you already know the lowest possible value for your roots is in (0,1) and the highest is in (1,2) How can you get an interval of sum of roots and product from this?

OK let me try

Let the roots of the equation f(x) = 0 be A and B. So:

A + B = -k and 1 < A + B < 3, then 1 < -k < 3 leads to -3 < k < -1

A.B = k² - 2k - 4 and 0 < AB < 2, then 0 < k² - 2k - 4 < 2
1. 0 < k² - 2k - 4 --> solving this, I got : k < 1 - √5 or k > 1 + √5

2. k² - 2k - 4 < 2 --> solving this, I got : 1 - √7 < k < 1 + √7

So the range of k for 0 < k² - 2k - 4 < 2 is 1 - √7 < k < 1 - √5 or 1 + √5 < k < 1 + √7


The intersection of -3 < k < -1 and (1 - √7 < k < 1 - √5 or 1 + √5 < k < 1 + √7) is 1 - √7 < k < 1 - √5

But if I remember correctly, the solution is (1 - √13) / 2 < k < 1 - √5

Where is my mistake?

Thanks

 

[Infinitum]

the curve f(x) intersects x axis(has 2 roots), what condition does this give you for the discriminant?

One condition comes also from the discriminant -3k²+8k+16. It can not be negative.

There you go.

 

[songoku]

It was Vieta! I could not remember the name.
One condition comes also from the discriminant -3k²+8k+16. It can not be negative.
So you have three condition for k...

ehild

There you go.

-3k²+8k+16 ≥ 0

Solving that, I got : -4/3 ≤ k ≤ 4 and that leads to the same solution as previous: 1 - √7 < k < 1 - √5

 

[ehild]

1-√7=-1.645. -4/3 = -1.333. 1-√5=-1.236. So what is the domain for k?

ehild

 

[Infinitum]

Edit again.

I just found a fatal problem with this method of using only Vieta formula and discriminant. In your cases you also consider the cases when both A and B are between (0.5,1) since addition and multiplication of these two numbers will satisfy the inequality you get. To rectify this, think about what the nature of f(1) should be? Refer my post #2 for that.

 

[songoku]

1-√7=-1.645. -4/3 = -1.333. 1-√5=-1.236. So what is the domain for k?

ehild

Edit : ehild replied

Oops sorry my bad. I thought 1 - √7 > -4/3

So, the domain for k is -4/3 < k < 1 - √5

But still it's not the same as the answer key, which is (1 - √13) / 2 < k < 1 - √5

How can we get term (1 - √13) / 2 from above working?

 

[Infinitum]

Please see post #12 again.

 

[songoku]

Please see post #12 again.

Sorry, when I posted, your post #12 consists only ehild replied

I found the answer thanks to your hint. But how can you know we need to eliminate the case [0.5 , 1]? And how can we be sure that there are no others fatal problems such as [0.5 , 1]?

If there was no answer key, I will answer -4/3 < k < 1 - √5 confidently

 

[Infinitum]

Sorry, when I posted, your post #12 consists only ehild replied

I found the answer thanks to your hint. But how can you know we need to eliminate the case [0.5 , 1]? And how can we be sure that there are no others fatal problems such as [0.5 , 1]?

If there was no answer key, I will answer -4/3 < k < 1 - √5 confidently

To see whether there is a problem, the best way is to see if you can find any example that will contradict your answer

The method I explained in post #2 is foolproof. You only need to be cautious.

 

[ehild]

I do not understand. Just the Vieta formulae were not enough. But we added the condition of the non-negativity of the discriminant with k.
It is not required that any pair from (0,1) and (1,2) be solutions.

The official solution is (1 - √13) / 2 < k < 1 - √5. Approximately it means -1.30<k<-1.23

We got -1.33<k<-1.23. And k=-1.32 is still appropriate.

ehild

 

[songoku]

To see whether there is a problem, the best way is to see if you can find any example that will contradict your answer

The method I explained in post #2 is foolproof. You only need to be cautious.

Sometimes it is pretty hard to find any example that will contradict the answer, such as this one, because -4/3 is not so much differs from (1 - √13) / 2

But I'll try to keep that in mind

By the way, I think using f(0) > 0 and f(1) < 0 will give correct result and it is faster ?? I got this idea from your post

 

[songoku]

I do not understand. Just the Vieta formulae were not enough. But we added the condition of the non-negativity of the discriminant with k.
It is not required that any pair from (0,1) and (1,2) be solutions.

The official solution is (1 - √13) / 2 < k < 1 - √5. Approximately it means -1.30<k<-1.23

We got -1.33<k<-1.23. And k=-1.32 is still appropriate.

ehild

I am not sure I get what you mean but substituting k = -1.32 to f(x) will result that the solution does not lie on interval (1,2)

 

[ehild]

I am not sure I get what you mean but substituting k = -1.32 to f(x) will result that the solution does not lie on interval (1,2)

Sorry, I miscalculated something. Infinitum is right.
But it was a nice problem...

ehild

 

[Infinitum]

Sometimes it is pretty hard to find any example that will contradict the answer, such as this one, because -4/3 is not so much differs from (1 - √13) / 2

But I'll try to keep that in mind

By the way, I think using f(0) > 0 and f(1) < 0 will give correct result and it is faster ?? I got this idea from your post

No. Thats not a necessary AND sufficient condition. Since you already found the answer, let me elaborate my method.

The graph of the given equation is an upward parabola.

Obviously, discriminant is greater than 0. Now from your conditions on roots, f(0) is positive, and so is f(2). So, their product will be positive(you can separately make two inequalities for each to be greater than 0, but I find this easier). Whence you get the inequality, f(0).f(2) > 0. The other condition is, f(1) < 0. The intersection of these three conditions will give you the answer.

But it was a nice problem...
ehild

Sure was!

 

[ehild]

It is a very nice and easy solution, if you have found it! Congratulation! Just a little note: f(2) = k^2, so it is obviously not negative. That product of f(0) and f(2) was a bit confusing.

ehild

 

[Infinitum]

It is a very nice and easy solution, if you have found it! Congratulation! Just a little note: f(2) = k^2, so it is obviously not negative. That product of f(0) and f(2) was a bit confusing.

ehild

Actually, this holds even if f(2) wasn't k^2. Here's why,

The graph of the parabola is upward, and it intersects x-axis in between (1,2). So, as the curve proceeds, it goes above 2, making f(2) positive in any situation. Same logic for f(0). And since products of positive numbers are always positive...

 

[ehild]

Actually, this holds even if f(2) wasn't k^2. Here's why,
.

All right, I know that both f(0) and f(2) have to be positive but why did you suggest the product? It complicates the problem and the product can be positive if both values are negative.

ehild

 

[Infinitum]

All right, I know that both f(0) and f(2) have to be positive but why did you suggest the product? It complicates the problem and the product can be positive if both values are negative.

ehild

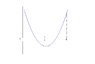
Ah, yes. I was trying to generalize the result , since if the coefficient of x^2 was negative, it would still imply the product of f(0) and f(2) would be positive. But it does include more cases, so it would be wise to consider each separately.

 

[songoku]

No. Thats not a necessary AND sufficient condition. Since you already found the answer, let me elaborate my method.

The graph of the given equation is an upward parabola.

Obviously, discriminant is greater than 0. Now from your conditions on roots, f(0) is positive, and so is f(2). So, their product will be positive(you can separately make two inequalities for each to be greater than 0, but I find this easier). Whence you get the inequality, f(0).f(2) > 0. The other condition is, f(1) < 0. The intersection of these three conditions will give you the answer.



Sure was!

Sorry, I don't get the part about necessary and sufficient condition. Which one is necessary and sufficient condition? And that proposition is necessary and sufficient condition to what proposition?

I hope I made myself clear

Thanks

 

[Infinitum]

Sorry, I don't get the part about necessary and sufficient condition. Which one is necessary and sufficient condition? And that proposition is necessary and sufficient condition to what proposition?

I hope I made myself clear

Thanks

The necessary condition is to include f(2) > 0, which you hadn't. And it is necessary to get the answer to your original question! Also, as I posted above, it would be better to use f(0) > 0, f(2) > 0, and f(1) < 0 since its more reliable.

 

[songoku]

The necessary condition is to include f(2) > 0, which you hadn't. And it is necessary to get the answer to your original question! Also, as I posted above, it would be better to use f(0) > 0, f(2) > 0, and f(1) < 0 since its more reliable.

Oh I see

Thanks a lot for the help