Solution space of nth order linear ODE, n dimension Vector Space

[popopopd]

if we do picard's iteration of nth order linear ODE in the vector form, we can show that nth order linear ODE's solution exists.

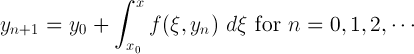(5)

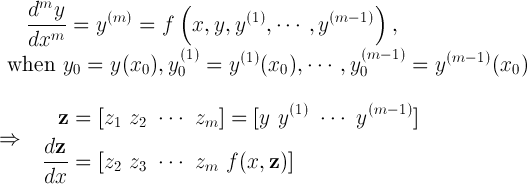(17)

example)

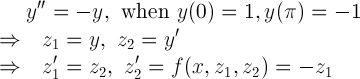(21)

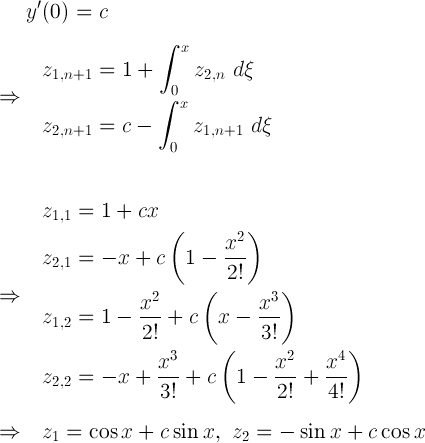(22)

(http://ghebook.blogspot.ca/2011/10/differential-equation.html)I found that without n number of initial conditions, the solution will not be unique because we assume initial conditions are some arbitrary constants. (example 22)

If we do picard's iteration without any initial conditions,

y(n-1)=y0(n-1)+∫y(n)dx
y(n-2)=y0(n-2)+∫y(n-1)dx
=y(n-2)=y0(n-2)+∫y0(n-1)+∫y(n)dx
.
.
.
iteration goes on and on until the error is sufficiently decreased.

if we assume each initial conditions are some arbitrary constants, we can sort out the solution function y w.r.t constants after sufficient number of iteration is done. Then it will look like,

y (c0 c1 c2 - - - - - - )[y1 y2 y3 y4 y5 - - - - - - ] <-- (should be vertical)which is in the form of y = c1y1+c2y2+c3y3 . . .
Since function space is vector space, solutions span n dimensional vector space.

is this correct?
If not, how can we show that solution space has n number of basis?
Also, how are we sure that general solutions are 'always' linearly independent? ---------------------------------------------------------------------------------------------------------------------------

Also, I have two questions about Strum Liouville 2nd order ODE.1. if we look at the Strum-Liouville 2nd order ODEs, there is an eigenvalue term within the equation. it seems like we are introducing one more constant to the equation, which imposes a restriction to find a solution (n+1 constants with n initial conditions).

[m(x)y']'+[λr(x)-q(x)]y
=m(x)[y''+P(x)y'+Q(x)y]
=m(x)[y''+P(x)y'+(λr(x)-q(x))]
=0

∴ [y''+P(x)y'+(λr(x)-q(x))]=0

if we do Picard's iteration, then we have one more constant λ along with n constants..2. I don't understand how eigenvalue directly influence the solutions of 2nd order ODE

 

[Lebesgue]

I do not fully understand the procedure of Picard's iteration, but the way I have proved in class that the solution space of the linear homogenous differential equation of nth order is a vector space of dimension n is the following:

First, we have that the ODE of order n is equivalent to an ODS (ordinary differential system) of order 1, which can be represented as y' = A·y since it is linear. (Where y is a vector function from ℝ to ℝ_n and A is an n by n matrix function defined on a subset of ℝ.)
Second, by Picard's existence and uniqueness theorem we have that choosen any t₀ from ℝ and chosen n basis vectors from ℝⁿ there exists a unique solution f_i of the problem y' = A·y and y(t₀) = e_i (the i-th basis vector).

Finally, we want to prove that B = {f₁,...f_n} is a basis of the solution space (proving it is a vector space is trivial). First, the set B is linearly independet since any linear combination of those functions, evaluated in t₀ forms a linear combination of a basis of ℝⁿ, so the scalar coefficients must all be zeroes. Finally, it spans the space for the uniqueness: given a function g solution of the ODS, and given w =g( t₀) a vector in ℝⁿ , there exist unique coefficients so that g( t₀) = ∑ f_i (t₀). Then, from the local uniqueness around the point t₀, the function g must be locally the function ∑ f_i, and then B spans V.

 

[HallsofIvy]

Picard's method can be used to show that a solution to an nth order differential equation, with given value of y and its first n-1 derivatives, exists and is unique.

To show that the solution set of an nth order homogeneous differential equation is an n dimensional vector space, you need to first show that the differential operator is linear: if y1 and y2 satisfy the equation then so does ay1+ by2 for any constants a and b. Then show that the specific solutions
a) y1 such that y1(x0)= 1, y'(x0)= y''(x0)= ...= y^(n-1)(x0)= 0
b) y2 such that y2(x0)= 0, y'(x0)= 1, y''(x0)= ...= y^(n-1)(x0)= 0
...
z) yn such that yn(x0)= y'(x0)= ...= y^(n-2)(x0)= 0, y^(n-1)(x0)= 1

form a basis for the solution space.