Solve F=ma Zip Line Problem: Angles & Sag

[Jae]

Question Info:
A fun way to cross a chasm is to use a so-called Zip Line as shown in the figure. Assume that the width of the chasm you are crossing is, 21m . The rope must sag sufficiently so it won't break. Assume the rope can provide a tension force of up to 26kNbefore breaking, and use a "safety factor" of 10 (that is, the rope should only be required to undergo a tension force of 2.6kN ) when you are in the position shown.(Figure 1)

Question:
Determine the sag in the rope, x , for the rope to match its recommended safety range. Assume that your mass is 75.0kg.

Diagram:

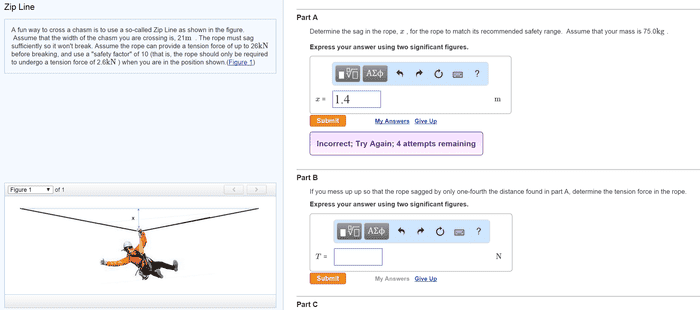
As I am trying to solve this problem, I can't seem to find the angle theta that would allow me to calculate x.

 

[SteamKing]

You are given the mass of the Zipliner, and you also know the maximum tension force allowed in the rope.

Start by drawing a free body diagram of this problem and work out the tension produced in each rope while
they are holding up the Zipliner. For now, the angle theta will be treated as an unknown until further analysis
can be done.

 

[Jae]

You are given the mass of the Zipliner, and you also know the maximum tension force allowed in the rope.

Start by drawing a free body diagram of this problem and work out the tension produced in each rope while
they are holding up the Zipliner. For now, the angle theta will be treated as an unknown until further analysis
can be done.

I tried drawing the free body diagram, but I don't see any way I can get theta without a spring constant. How can this be done without the spring constant? Thank you for your time.

 

[SteamKing]

Yes. The stretch in the rope caused by the maximum allowable tension is assumed to be negligible, i.e. treat the lines as if they
are rigid bodies.

 

[Jae]

Yes. The stretch in the rope caused by the maximum allowable tension is assumed to be negligible, i.e. treat the lines as if they
are rigid bodies.

If the stretch is negligible, how can I calculate x?

 

[SteamKing]

If the stretch is negligible, how can I calculate x?

What you are trying to determine is the tension in the ropes, not the amount of stretch. You are over analyzing this problem.

You know the weight of the guy hanging off the line and the total distance between supports. It basically comes down to resolving the weight of the Zipliner into each rope, and figuring out the maximum sag 'x' which keeps the calculated tension in each rope below the allowable value.

 

[Jae]

What you are trying to determine is the tension in the ropes, not the amount of stretch. You are over analyzing this problem.

You know the weight of the guy hanging off the line and the total distance between supports. It basically comes down to resolving the weight of the Zipliner into each rope, and figuring out the maximum sag 'x' which keeps the calculated tension in each rope below the allowable value.

So the 75 * 9.81 = 735.75N divided by 2 is 367.875N. The only way I can think to find an angle here is by doing arctan (736/368), but that's the angle of the forces. How would I find the negligible angle that would allow me to find x?

 

[SteamKing]

So the 75 * 9.81 = 735.75N divided by 2 is 367.875N.

This is OK.

Now remember what the problem statement told you: you want to find the maximum sag 'x' so that the tension in each rope does not exceed 2.6 kN. How do you use this restriction in your calculations?