- #1
Dimani4
- 50
- 0
Hi all,
I still have "a many times discussed" problem to understand Feymann's issue about irreversible/reversible machines example.
Here is the part from the original text.
Here is my questions:
1. Here Feymann talks about the situation when you are not applying any force to rise or lower the weight. Your system is closed (isolated) for any applying force, you only supply the weights for the system. Let's talk about irreversible machine like Feymann says
Take a look at the picture of the real irreversible machine:
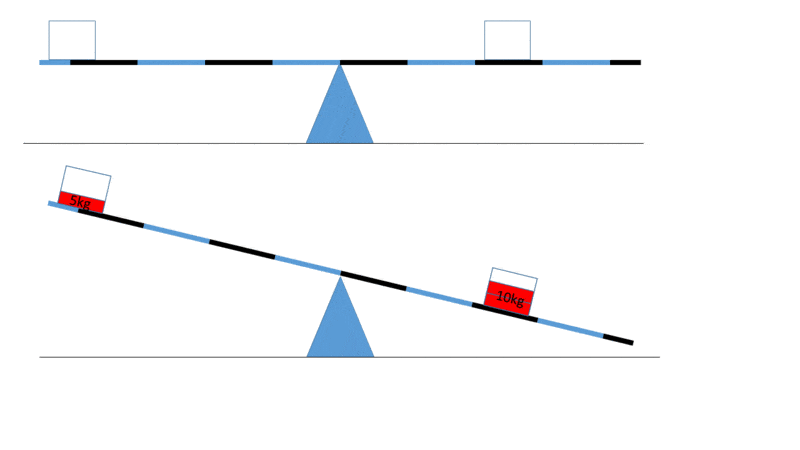
here the link which could help: https://phet.colorado.edu/sims/html/balancing-act/latest/balancing-act_en.html
The first picture is perfectly balanced condition with baskets for weights. Let's neglect the weights of baskets and weight of lever and friction of fulcrum. Now, we put the weights into the baskets and then we have 5kg is lifted and 10 kg is lowered. Now we remove the weights and the scales back to the balanced condition. So we didnt apply any energy to lift the weight and the system back to the initial condition and in the end we succeeded to arise the weight that can do something else (as Feynman says)
I still have "a many times discussed" problem to understand Feymann's issue about irreversible/reversible machines example.
Here is the part from the original text.
We imagine that there are two classes of machines, those that are not reversible, which includes all real machines, and those that are reversible, which of course are actually not attainable no matter how careful we may be in our design of bearings, levers, etc. We suppose, however, that there is such a thing—a reversible machine—which lowers one unit of weight (a pound or any other unit) by one unit of distance, and at the same time lifts a three-unit weight. Call this reversible machine, Machine A. Suppose this particular reversible machine lifts the three-unit weight a distance X. Then suppose we have another machine, Machine B, which is not necessarily reversible, which also lowers a unit weight a unit distance, but which lifts three units a distance Y. We can now prove that Y is not higher than X; that is, it is impossible to build a machine that will lift a weight any higher than it will be lifted by a reversible machine. Let us see why. Let us suppose that Y were higher than X. We take a one-unit weight and lower it one unit height with Machine B, and that lifts the three-unit weight up a distance Y. Then we could lower the weight from Y to X, obtaining free power, and use the reversible Machine A, running backwards, to lower the three-unit weight a distance X and lift the one-unit weight by one unit height. This will put the one-unit weight back where it was before, and leave both machines ready to be used again! We would therefore have perpetual motion if Y were higher than X, which we assumed was impossible. With those assumptions, we thus deduce that Y is not higher than X, so that of all machines that can be designed, the reversible machine is the best.
Here is my questions:
1. Here Feymann talks about the situation when you are not applying any force to rise or lower the weight. Your system is closed (isolated) for any applying force, you only supply the weights for the system. Let's talk about irreversible machine like Feymann says
Here in the case of irreversible machine we don't supply any energy to rise the weight. But if we do not supply the energy and the machine returns to the initial state and in the end the weight is raised we have the perpetual movement.those that are not reversible, which includes all real machines,
Take a look at the picture of the real irreversible machine:
here the link which could help: https://phet.colorado.edu/sims/html/balancing-act/latest/balancing-act_en.html
The first picture is perfectly balanced condition with baskets for weights. Let's neglect the weights of baskets and weight of lever and friction of fulcrum. Now, we put the weights into the baskets and then we have 5kg is lifted and 10 kg is lowered. Now we remove the weights and the scales back to the balanced condition. So we didnt apply any energy to lift the weight and the system back to the initial condition and in the end we succeeded to arise the weight that can do something else (as Feynman says)
. So we have perpetual motion (according Feynman definition) here? If we do it again we will lift another 5kg and again 5kg...we can use that lifted weight to run something else.
If, when we have lifted and lowered a lot of weights and restored the machine to the original condition, we find that the net result is to have lifted a weight, then we have a perpetual motion machine because we can use that lifted weight to run something else.
