Konig
- 6
- 0
Hi, need help solving a first order homogeneous ODE.
y'(x)-(a/x)y = b/(x(1+x)^2) Here a and b are some constants.
Need to solve this for y.
My attempts so far have been to use
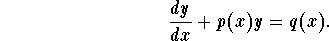
But this means solving ∫ x^(-a)/(x(1+x)^2) dx which has solutions in terms of Gauss hyper-geometric functions,
http://en.wikipedia.org/wiki/Hypergeometric_function"
Which lead me to believe I'm going wrong somewhere...
Sorry for the maths format, I'm new to here and don't know how to insert LaTeX.
Thanks
y'(x)-(a/x)y = b/(x(1+x)^2) Here a and b are some constants.
Need to solve this for y.
My attempts so far have been to use
But this means solving ∫ x^(-a)/(x(1+x)^2) dx which has solutions in terms of Gauss hyper-geometric functions,
http://en.wikipedia.org/wiki/Hypergeometric_function"
Which lead me to believe I'm going wrong somewhere...
Sorry for the maths format, I'm new to here and don't know how to insert LaTeX.
Thanks
Last edited by a moderator: