Solve Geometry Problem for Senior Design Project

[Abyss]

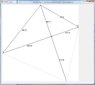
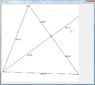
Hi guys, I'm doing my senior design project and we've decided upon a method for finding the location of our robot in the square arena that we have built. The method we are using involves sensors on all four sides of the robot (each at 90 degrees of the two adjacent) that return the distance to one of the straight walls of the arena.

I am sure that given the 4 lengths from the robot to the walls of the arena, and knowing the angle that the robot is at, that it is possible to find the location the robot is at. I've spent a couple days on this problem though, and I haven't been able to come up with a general solution.

I know that with about 200 if-else statements I could program a solution but we need our code to be as elegant as possible.

I have a dozen pages of notes, and I have written an application to help me visualize the problem and test potential solutions, if anyone has any ideas I'd love to hear them.

I attached two pictures of the app, but they really aren't necessary, they may help explain the problem more clearly though.

 

[I like Serena]

A possible solution is to write a function that given an input (x,y,phi) calculates the 4 distances to the wall.
You can do this by intersecting the lines with all the walls.
In each heading you need the nearest intersection that lies in the proper direction.

Then write a second function that approximates your position.
That is:
1. start in the middle with your angle phi.
2. calculate the 4 distances
3. take a small step in the direction with the greatest mismatch
4. repeat 2 & 3 until you cannot get closer any more
5. if your mismatches are reasonably small you have found your position.

 

[Abyss]

Thanks for the suggestion, I agree that solution would work. In fact we use something similar in our inverse kinematic solution.

In the end after working with it some more I decided to find all the possible solutions that a single sensors distance/angle could return per quadrant (which look like two line segments connected in a right angle). Then intersect those elbows until a solution is found.

It isn't perfect but elegant enough for my tastes. I've included a screeny which looks quite complicated but alas no graphical depiction of this problem will be simple. The solution for sensor A (in direction of the robot depicted by a small circle a short distance away from the central circle) is in Red, the solution for sensor B is +90 off of sensor A and is green, the solution for C is 180 off of A and is blue and the solution for D is 270 off of A and is yellow. The region enclosed by each solution is shaded in the solutions color, which can help to highlight the different solutions.

 

[I like Serena]

Thanks for the suggestion, I agree that solution would work. In fact we use something similar in our inverse kinematic solution.

In the end after working with it some more I decided to find all the possible solutions that a single sensors distance/angle could return per quadrant (which look like two line segments connected in a right angle). Then intersect those elbows until a solution is found.

It isn't perfect but elegant enough for my tastes. I've included a screeny which looks quite complicated but alas no graphical depiction of this problem will be simple. The solution for sensor A (in direction of the robot depicted by a small circle a short distance away from the central circle) is in Red, the solution for sensor B is +90 off of sensor A and is green, the solution for C is 180 off of A and is blue and the solution for D is 270 off of A and is yellow. The region enclosed by each solution is shaded in the solutions color, which can help to highlight the different solutions.

That works too. As yet I don't see a more elegant solution.

Note that I expect that you won't be able to keep your phi accurate.
So I think you'll need to use your measurements too to correct phi back to the proper angle.