Solve Particle Equilibrium Homework Statement

[Robb]

Homework Statement

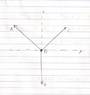
If the 4.4-kg block is suspended from the pulley B and the sag of the cord is d = 0.15 m, determine the force in cord ABC. Neglect the size of the pulley. (Figure 1)
Express your answer to three significant figures and include the appropriate units.

Homework Equations

The Attempt at a Solution

[/B]
r(BC) = (x^2 + .15^2)^.5
r(AB) = [(.4-x)^2 + (.15^2)]

T(x) = r(BC)cos(theta) - r(AB)cos(theta)
T(y) = r(BC)sin(theta) + r(AB)sin(theta) - 43.164

I tried adding r(BC) + r(AB) and then grphing to find the zeros but that was wrong.

I also have; x/cos(theta) + .4-x/cos(theta) = .4cos(theta)

not sure how to proceed.

 

[BvU]

Hi Robb,

Is there a reason to assume $x\ne0.2$ m ?

 

[Robb]

Can I assume it's centered?

 

[haruspex]

Can I assume it's centered?

You are given that A and C are on the same horizontal level. You have correctly presumed that the angle is the same each side (if anything, that was the step that needs some physics to justify). If the vertical through B meets AC at E, what can you say about triangles AEB, CEB?

 

[Robb]

I suppose they are equal. I guess I don't like to make that assumption without proof. I suppose they would have to be though, given that the pulley would be assumed to be frictionless. Is that a correct assumption?

 

[haruspex]

I suppose they are equal. I guess I don't like to make that assumption without proof. I suppose they would have to be though, given that the pulley would be assumed to be frictionless. Is that a correct assumption?

Yes. If there were static friction in the pulley then there would be a range of answers.

 

[Robb]

So, shouldn't T(ABC) = -43.164N?

 

[haruspex]

So, shouldn't T(ABC) = -43.164N?

Not what I get, and it certainly cannot be negative.
Please post your working.

 

[Robb]

F(x) = 0; F(BC)cos37 - F(BA)cos37
F(y) =0; F(BC)sin37 + F(BA)sin37 - 43.164
F(BC) = F(BA)
-.6435F(BC) - .6435F(BC) = 43.164
F(BC) = 33.5359N

 

[haruspex]

F(x) = 0; F(BC)cos37 - F(BA)cos37
F(y) =0; F(BC)sin37 + F(BA)sin37 - 43.164
F(BC) = F(BA)
-.6435F(BC) - .6435F(BC) = 43.164
F(BC) = 33.5359N

Ok.
Two issues.
1. Where did those minus signs come from in the line before last (which you then ignored to get the last line)?
2. There is no need to find the angle. Doing so has introduced some rounding error. The sine and cosine are exactly 0.6 and 0.8.

 

[Robb]

1. good question

I see what you're saying about not needing the angle.

F(x)=0; F(BC)(0.8) - F(BA)0.8)= 0
F(y)=0; F(BC)(0.6) + F(BA)(0.6) -43.164=0

F(BC)=F(BA)
1.2F(AC) = 43.164
F(AC) = 35.97

I assume this is the force in cord ABC?

 

[haruspex]

1. good question

I see what you're saying about not needing the angle.

F(x)=0; F(BC)(0.8) - F(BA)0.8)= 0
F(y)=0; F(BC)(0.6) + F(BA)(0.6) -43.164=0

F(BC)=F(BA)
1.2F(AC) = 43.164
F(AC) = 35.97

I assume this is the force in cord ABC?

Yes. But I would not have written F(AC); that's a bit confusing since there is nothing acting along the straight line AC. You could write F(ABC), or just leave it as F(AB).