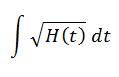The discussion revolves around converting an equation involving the Heaviside step function, H(t), into the s-domain using the Laplace transform. The user seeks clarification on whether H(t) is indeed the Heaviside step function, indicating uncertainty about its application in their specific problem. They clarify that in their context, H(t) represents the height of the water level, which varies over time. Participants are encouraged to provide assistance with the Laplace transform process. The conversation highlights the need for clear definitions and understanding of terms in mathematical transformations.