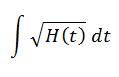Solve Surds Using Laplace Transform

  • Thread starter Thread starter yuri6996
  • Start date Start date
AI Thread Summary
The discussion revolves around converting an equation involving the Heaviside step function, H(t), into the s-domain using the Laplace transform. The user seeks clarification on whether H(t) is indeed the Heaviside step function, indicating uncertainty about its application in their specific problem. They clarify that in their context, H(t) represents the height of the water level, which varies over time. Participants are encouraged to provide assistance with the Laplace transform process. The conversation highlights the need for clear definitions and understanding of terms in mathematical transformations.
yuri6996
Messages
2
Reaction score
0
can anyone advise me any way to convert this equation to s-domain by using laplace transform
TQ...

laplacesurd.jpg
 
Last edited:
Mathematics news on Phys.org
H(t) is the Heaviside step function? Well, \sqrt{0}= 0 and \sqrt{1}= 1 so \sqrt{H(t)}= H(t)!
 
err HallsofIvy
are u asking me that the H(t) is the Heaviside step function or not
because actually i didnt know

the H(t) in my problem is the height of the water level
its differ with time

hope u can assist me
TQ in advance...
 
Thread 'Video on imaginary numbers and some queries'

Thread 'Video on imaginary numbers and some queries'

Hi, I was watching the following video. I found some points confusing. Could you please help me to understand the gaps? Thanks, in advance! Question 1: Around 4:22, the video says the following. So for those mathematicians, negative numbers didn't exist. You could subtract, that is find the difference between two positive quantities, but you couldn't have a negative answer or negative coefficients. Mathematicians were so averse to negative numbers that there was no single quadratic...
View full post »

Thread 'What Exactly is Dirac’s Delta Function? - Insight'

Insights auto threads is broken atm, so I'm manually creating these for new Insight articles. In Dirac’s Principles of Quantum Mechanics published in 1930 he introduced a “convenient notation” he referred to as a “delta function” which he treated as a continuum analog to the discrete Kronecker delta. The Kronecker delta is simply the indexed components of the identity operator in matrix algebra Source: https://www.physicsforums.com/insights/what-exactly-is-diracs-delta-function/ by...
View full post »

Thread 'Non-orthogonal bases'

Suppose ,instead of the usual x,y coordinate system with an I basis vector along the x -axis and a corresponding j basis vector along the y-axis we instead have a different pair of basis vectors ,call them e and f along their respective axes. I have seen that this is an important subject in maths My question is what physical applications does such a model apply to? I am asking here because I have devoted quite a lot of time in the past to understanding convectors and the dual...
View full post »

Similar threads

MHB Inverse laplace transform pf infinite product
Replies
1
Views
1K
I Region of convergence of a Laplace transform
Replies
1
Views
2K
I Convergence of this Laplace transformation
Replies
3
Views
2K
Laplace transform vs phasor analysis in circuit analysis
Replies
3
Views
2K
Engineering How would I solve this using Laplace transformation?
Replies
4
Views
2K
How Do Laplace Transforms Help Understand Frequency and Amplitude in Signals?
Replies
3
Views
3K
What is the best way to introduce Laplace transforms for Engineers?
Replies
10
Views
3K
MHB What is the best way to introduce Laplace transforms in an Engineering Mathematics course?
Replies
7
Views
5K
My engineering faculty is having us rote-memorize Laplace transforms
Replies
1
Views
2K
MHB Adam's question via email about Laplace Transforms
Replies
4
Views
11K

Hot Threads

Recent Insights

Back
Top