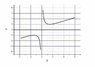
The equation x² + (√8)x*sin[(√2)xy] + 2 = 0 can be transformed into the form (x + √2sin(√2xy))² = -2 + 2sin²(√2xy). It is suggested to isolate y, leading to y = (1/√2x)arcsin(- (x² + 2)/(2√2x)), with the arcsin argument constrained to the range [-1, 1]. The transformation indicates that both sides of the equation must equal zero, resulting in two equations: x + √2sin(√2xy) = 0 and sin²(√2xy) = 1. The analysis reveals that x must be limited to specific values, with extrema occurring at x = ±√2, which determine the valid range for x.