OhMyGod
- 5
- 0
[SOLVED] Pressure (Barometer)
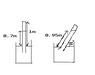
A mercury barometer of height 1.000m has some ideal gas trapped inside. When the tube is vertical, the height of the mercury column is 0.700m. When the tube is inclined at an angle of 30 degrees to the horizontal, the length of the mercury is 0.950m.
Assuming temperature is constant, the atmospheric pressure, in mm Hg, is ?
(a picture of the question is attached)
Answer: 745mmHg
Pressure = hpg
I tried working it along this line whereby Atmospheric Pressure = Pressure of the ideal gas(hpg) + Pressure of vertical length of Mercury .
Formed 2 simultaneous equations with the 2 diagrams as attached. But no luck in getting the answer so far. Please tell me whether the direction that I am going at is correct.
Thanks in advance :D
Homework Statement
A mercury barometer of height 1.000m has some ideal gas trapped inside. When the tube is vertical, the height of the mercury column is 0.700m. When the tube is inclined at an angle of 30 degrees to the horizontal, the length of the mercury is 0.950m.
Assuming temperature is constant, the atmospheric pressure, in mm Hg, is ?
(a picture of the question is attached)
Answer: 745mmHg
Homework Equations
Pressure = hpg
The Attempt at a Solution
I tried working it along this line whereby Atmospheric Pressure = Pressure of the ideal gas(hpg) + Pressure of vertical length of Mercury .
Formed 2 simultaneous equations with the 2 diagrams as attached. But no luck in getting the answer so far. Please tell me whether the direction that I am going at is correct.
Thanks in advance :D