Solving a circuit using laplace transform

[magnifik]

For the circuit below, find the V_a(s)

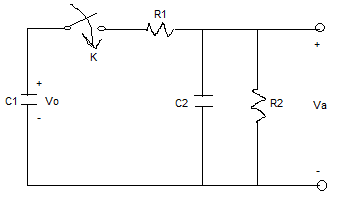
What I have done so far:
I attempted to solve using the node method when the switch is closed (t > 0)
(v_a - v₀)/R₁ + C₂dv_a/dt + v_a/R₂ = 0

After a series of calculations I got
V_a(s) = (V₀/C₂R₁)*(1/s+(1/C₂R₁) + (1/C₂R₂))

What I am unsure of is if my first equation is correct. I did not account for C₁; I simply used the fact that the voltage across it was v₀.

 

[vela]

It's not correct. Consider how the circuit responds if C₁ is very large so the voltage across it doesn't change very quickly. What if C₁ is very small so even a small current can cause its voltage to change quickly? Obviously, the response of the system will have to depend on how big C₁, so that quantity must appear in your solution.

Have you learned about writing the impedance of elements in the s-domain and then treating everything like a resistor? That would be the most straightforward way to solve the problem.

 

[magnifik]

It's not correct. Consider how the circuit responds if C₁ is very large so the voltage across it doesn't change very quickly. What if C₁ is very small so even a small current can cause its voltage to change quickly? Obviously, the response of the system will have to depend on how big C₁, so that quantity must appear in your solution.

Have you learned about writing the impedance of elements in the s-domain and then treating everything like a resistor? That would be the most straightforward way to solve the problem.

I haven't learned about that.
So my first equation isn't correct at all? Or can I also have a separate equation, C₁dv₀/dt = 0 and combine the two equations in the end? I haven't tried this method yet so I'm not sure if it makes any sense. Thanks for the help.

 

[vela]

Your first equation is correct, but when you went to the s-domain, I think you assumed V₀ is a constant, which it isn't. That's how the dependence on C₁ enters in.

 

[gneill]

At the risk of seeming to cause more work, label a new node between C1 and R1. Let's say that the voltage there is V1. Now you can write a KCL equation for each node. Ignore Vo to begin with; when you take the Laplace transforms of the equations you'll soon see where to plug it in!

 

[magnifik]

At the risk of seeming to cause more work, label a new node between C1 and R1. Let's say that the voltage there is V1. Now you can write a KCL equation for each node. Ignore Vo to begin with; when you take the Laplace transforms of the equations you'll soon see where to plug it in!

So to solve for V₁ I did the following:
C₁(dv₁/dt) + (v₁ - v_a)/R₁ = 0
which turns into
C₁[sV₁(s) - v₁(0^-)] + (V₁(s) - V_a(s))/R₁ = 0
I solved for V₁ and got
V_a(s)/(C₁s + 1)

I believe the next step would be that I plug this in for V₀ in my original equation.

 

[gneill]

V1(0) should be the initial voltage on C1 (that is, Vo). The result of solving this equation for V1(s) should also include R1 in its makeup. What happened to Vo and R1?

When you have this sorted out, yes, plug the expression for V1(s) into your other equation so that you can solve for Va(s). Then it's inverse Laplace time!

 

[magnifik]

V1(0) should be the initial voltage on C1 (that is, Vo). The result of solving this equation for V1(s) should also include R1 in its makeup. What happened to Vo and R1?

When you have this sorted out, yes, plug the expression for V1(s) into your other equation so that you can solve for Va(s). Then it's inverse Laplace time!

Ah yes, I made a typo. I actually got
V₁(s) = V_a(s)/(C₁R₁s + 1)
but when I plug in 0 for s, I get V1(0) = Va(0) which makes no sense to me unless you were taking about v1(0-), in which case it is 0 since the voltage is 0 initially

 

[gneill]

Ah yes, I made a typo. I actually got
V₁(s) = V_a(s)/(C₁R₁s + 1)
but when I plug in 0 for s, I get V1(0) = Va(0) which makes no sense to me unless you were taking about v1(0-), in which case it is 0 since the voltage is 0 initially

The capacitor is initially charged to voltage Vo, according to your circuit diagram.

 

[magnifik]

The capacitor is initially charged to voltage Vo, according to your circuit diagram.

Oh, I see what you're saying...I think. So V₀ should be in my equation for V₁(s)? I initially thought the capacitor C₁ had a voltage of 0, which is why I was confused.

 

[gneill]

Oh, I see what you're saying...I think. So V₀ should be in my equation for V₁(s)? I initially thought the capacitor C₁ had a voltage of 0, which is why I was confused.

Yes, I think you have it now! The diagram showed Vo on the capacitor. That value should be inserted for V1(0) in your expressions.

 

[magnifik]

Ok, I think I finally got the answer. It's a bit messy though. I just have one last question regarding this problem: am I correct in assuming that Va(0) = 0?

 

[gneill]

Ok, I think I finally got the answer. It's a bit messy though. I just have one last question regarding this problem: am I correct in assuming that Va(0) = 0?

You are indeed correct! While the switch is open before t=0, capacitor C2 will be discharged via R2.

 

[magnifik]

Thank you for all the help! Much appreciated!