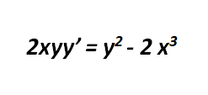Cadbury
- 11
- 0
Hi! So I am solving this problem:
View attachment 3777
Find the solution that passes through (1,2)
First I tried substituting
x= u+1
y= v+2
dx = du
dy = dv to the equation but I cannot find the solution any help will be appreciated, thank you! :D
View attachment 3777
Find the solution that passes through (1,2)
First I tried substituting
x= u+1
y= v+2
dx = du
dy = dv to the equation but I cannot find the solution any help will be appreciated, thank you! :D
Attachments
Last edited: