Solving a Non-Exact O.D.E. with Coordinate Axis Shift

[asdf1]

(2x-4y+5)y` +x-2y+3=0

I've tried shifting the coordinate axis, but it doesn't work!
It's also not exact...

 

[TD]

You can write this as

y' = \frac{{ - x + 2y - 3}}{{2x - 4y + 5}}

Now you can see nominator and denominator as two lines. Normally, you'd shift to the intersection but these lines are parallel (since \frac{{ - 1}}{2} = \frac{2}{{ - 4}})

Now, write it as

y' = \frac{{ - x + 2y - 3}}{{ - 2\left( { - x + 2y} \right) + 5}}

And do the substitution u = - x + 2y

Your DE should become separable now.

 

[saltydog]

You know Asdf (and TD), gonna' end up with another messy solution (as I see it anyway). You can get there right Asdf? You know, make the substitutiion above, little of this, little of that, and we end up with:

y=\frac{3}{4}ln\left[11-4(2y-x)\right]+\frac{1}{4}(2y-x)+\frac{11}{16}ln\left[11-4(2y-x)\right]+c

See what I mean. Same boat as the other one. So I'd say treat it parametrically, that is:

\frac{dy}{dt}=-x+2y-3

\frac{dx}{dt}=2x-4y+5

This time, let's solve it with differential operators:

Rearranging:

<br /> \begin{align*}<br /> y^{&#039;}-2y+x&amp;=-3 \\<br /> \\<br /> 4y+x^{&#039;}-2x&amp;=5<br /> \end{align}<br />

Expressing these in terms of differential operators:

<br /> \begin{align*}<br /> (D-2)y&amp;+ x &amp;= -3 \\<br /> \\<br /> 4y &amp;+ (D-2)x &amp;= 5<br /> \end{align}<br />

Now just "operate" on them to eliminate y and x and end up with two second-order (non-homogeneous) ODEs for x(t) and y(t).

You familiar with this method?

 

[GCT]

are you sure its not exact?

 

[saltydog]

are you sure its not exact?

For:

(x-2y+3)dx+(2x-4y+5)dy=0

\frac{\partial}{\partial y}(x-2y+3)=-2

\frac{\partial}{\partial x}(2x-4y+5)=2

 

[Hurkyl]

Educated guessing yields a simpler solution than last time: if you try y = mx + b, you get y = x/2 + 11/8. (The other linear solution is singular! How amusing to have a singular singular solution. At least I feel that these linear solutions are singular in some sense)

I notice that this one is halfway between the two lines...

 

[asdf1]

hmm... I didn't think to make that substitution... but it simplies the equation~
i did think trying to parameterize it, except that i had a hard time on it~

 

[saltydog]

Educated guessing yields a simpler solution than last time: if you try y = mx + b, you get y = x/2 + 11/8. (The other linear solution is singular! How amusing to have a singular singular solution. At least I feel that these linear solutions are singular in some sense)

I notice that this one is halfway between the two lines...

Edit: The linear solutions are NOT singular solutions. See discussion below

Thanks Hurkyl. I had no idea. Your solution y=x/2+11/8 is indeed a singular solution by virtue that it is not a particulr case of the general solution and is an envelop of the general solution as per the attached plot which shows 7 solutions of the 1-parameter general solution all of which are tangent to the singular solution. That it, the singular solution is an envelop of the general solution. Can you answer this for me:

1. How does one know if an ODE will have a singular solution and how does one calculate it analytically (that is, without guessing)?

2. What do you mean by the "other linear solution"?

2. What do you mean by "singular singular solution"?

Added plots:

Plot 2: typical solution below singular solution

Plot 3: Solutions showing vertical tangent when denominator of ODE is 0 that is, whenever y=x/2+5/4

 

[Hurkyl]

When I plug in y = mx + b and solve, I get two equations. The first is quadratic in m, and the second is linear in b (with coefficients depending on m). This system ought to have two solutions, but when I use the second solution for m, m = -1/2, it kills the b in the other equation, rendering it inconsistent.

So the second linear "solution" is y = -x/2 + ∞.

Note that all of the nonsingular solutions are tangent to this one too!


I don't know, in general, how to spot the singular solutions.

However, in this case, we can find some information by looking asymptotically. When x and y are very large, we have:

(2x - 4y) y' + (x - 2y) = 0
(x - 2y) (2y' + 1) = 0

So there are two options for asymptotic behavior:
(1) y' ~ -1/2
(2) x - 2y ~ 0

There ought to be singular solutions that follow only one of the asymptotes. In this case, we're lucky, because those solutions are the asymptotes themselves:

(1) y = (-1/2)x + b
(2) y = (1/2)x + b


Ooh, cool idea. I decided this suggests using:

y(x) = (1/2) x + e(x)

Solving this for the general solution gives:

y = C - (1/2) x - (1/8) ln |y - (1/2) x - (11/8)|

If I assume that e(x) is not the constant (11/8).

Which suggests a nice closed form of the type y = f(x) is impossible. However, we can read off the behavior from this!

The function generally either looks like:
y = C - (1/2) x
or
y = (1/2) x + (11/8)

which is exactly what the asymptotic analysis told us. We could pin down further details too... for instance, the y = (1/2) x + (11/8) behavior asymptotically occurs in the direction of positive x.

 

[saltydog]

I find this so confusing:

Solving for the parametric solutions (which I'll post the details later), I obtain:

x(t)=c_1-1/2t+c_2e^{4t}

y(t)=d_1-1/4t+d_2e^{4t}

Where the constants are all functions of a single initial condition: y(x_0)=y_0

Forming the quotient of the respective derivatives I obtain:

\frac{dy}{dx}=\frac{-1/4+4d_2e^{4t}}{-1/2+4c_2e^{4t}}

Now this is the definition of a singular solution as per Rainville and Bedient:

(a) is not a special case of the general solution

(b) is, at each of its points, tangent to some element of the one-parameter family that is the general solution.


But the derivative above is NEVER equal to the derivative of the singular solutions y=x/2+11/8 and y=-x/2+\infty except at t=\pm \infty. That is:

\mathop\lim\limit_{t\to\pm \infty}\frac{-1/4+4d_2e^{4t}}{-1/2+4c_2e^{4t}}=\mp 1/2

The limit as t\to+\infty is due to the algebraic relation between the constants. For example, the case y(0)=a, the constants are:

c_2=11/8-a

d_2=\frac{a}{2}-\frac{11}{16}


I don't understand how then could the linear solutions be truly singular solutions when the only point of tangency is at infinity.

 

[Hurkyl]

Then I suppose it's not singular, then.

Doesn't my linear solution arise when c2 = d2 = 0?

 

[saltydog]

Then I suppose it's not singular, then.

Doesn't my linear solution arise when c2 = d2 = 0?

Sure looks like it Hurkyl although c2 and d2 being zero affects what c1 and d1 can be which in turn limits what the initial condition can be. I'll work it through. Thanks!

 

[saltydog]

Sure looks like it Hurkyl although c2 and d2 being zero affects what c1 and d1 can be which in turn limits what the initial condition can be. I'll work it through. Thanks!

Alright it works out. Through the parametric analysis, I got for the constants in the case y(0)=a:

c_1=a-11/8

c_2=-c_1

d_2=a/2-11/16

d_1=a-d_2

Which if d_2=c_2=0, that leaves a=11/8 which when solving for t in the expression for x(t) and substituting in for y(t) yield the solution:

y(x)=11/8+\frac{1}{2} x

Nice!

 

[Hurkyl]

critical!

That's the word I was looking for: my linear solution is a critical solution, because it lies on the boundary between the two types of behavior.

Now, I just need to figure out, generally, what being critical means with respect to the algebra.

 

[saltydog]

I'd like to better understand the relation of this system:

\frac{dx}{dt}=Ax+By+E

\frac{dy}{dt}=Cx+Dy+F

to this system:

\frac{dx}{dt}=ax+by

\frac{dy}{dt}=cx+dy

I understand when AD-BC\ne0, the first system can be converted to the second with the eigenvalues of the second system governing its dynamics. But how is this dynamics related to the original system? Is it the same?

I think all of this is related somehow. Suppose in summary I should ask: How can one determine the global behavior of the first system and can the dynamics be catagorized like that for the second system?

Also in the case of the second system, the straight-line solutions are the eigenvectors of the system. How is that related to the straight-line solution:

y(x)=x/2+11/8

for the system studied in this thread?

 

[saltydog]

I wish to make a conjecture:

Consider the system:

\frac{dx}{dt}=2x-4y+a

\frac{dy}{dt}=-x+2y+b

of which the problem above is a special case of a=5 and b=-3.

If a and b are zero, then this reduces to the second kind of linear system with eigenvalues 0 and 4. Thus the general solution for this case is:

<br /> \left(\begin{array}{c} x(t) \\<br /> y(t)<br /> \end{array}\right)=k_1<br /> \left(\begin{array}{c} x_1 \\<br /> y_1<br /> \end{array}\right)+k_2e^{4t}<br /> \left(\begin{array}{c} x_2 \\<br /> y_2<br /> \end{array}\right)<br />

Note this is very similar to the solution with the case a=5 and b=-3. In fact, I could write that case in matrix form as:

<br /> \left(\begin{array}{c} x(t) \\<br /> y(t)<br /> \end{array}\right)=k_1<br /> \left(\begin{array}{c} x_1 \\<br /> y_1<br /> \end{array}\right)+k_2e^{4t}<br /> \left(\begin{array}{c} x_2 \\<br /> y_2<br /> \end{array}\right)+k_3t<br /> \left(\begin{array}{c} x_3 \\<br /> y_3<br /> \end{array}\right)<br />

Thus I suggest investigating (me anyway) if the general solution of:

\frac{dx}{dt}=Ax+By+E

\frac{dy}{dt}=Cx+Dy+F

consist of a "homogeneous" part obtained from the solution of:


\frac{dx}{dt}=Ax+By

\frac{dy}{dt}=Cx+Dy

and a non-homogeneous part determined by the values of a and b and having the form:

<br /> k_3t<br /> \left(\begin{array}{c} x_3 \\<br /> y_3<br /> \end{array}\right)<br />

 

[Hurkyl]

Also, when AD-BC=0 as the case above, then we really have no eigenvalues to determine its behavior.

Yes you do.


Let's look at this one again:

x' = -2x + 4y
y' = x - 2y

a.k.a.

x' = A x with

A := \left(<br /> \begin{array}{cc}<br /> -2 &amp; 4 \\<br /> 1 &amp; -2<br /> \end{array}<br /> \right)<br />

We compute the characteristic equation of A:

f(\lambda) = \left|<br /> \begin{array}{cc}<br /> \lambda + 2 &amp; -4 \\<br /> -1 &amp; \lambda + 2<br /> \end{array}<br /> \right|<br /> = (\lambda + 2)^2 - 4 = \lambda^2 + 4\lambda = \lambda(\lambda + 4)<br />

so its two eigenvalues are 0 and -4.

The eigenvector associated to -4 is [2, -1]^T
The eigenvector associated to 0 is [2, 1]^T

So the general solution should be, I suppose,

x = A exp(0 t) [2, 1]^T + B exp(-4 t) [2, -1]^T
x = A [2, 1]^T + B exp(-4 t) [2, -1]^T

This looks right, I think. We recover the translational symmetry observed in the solutions.

Of course, that first base solution is unsatisfying. But it comes from an assumption I made in setting up the problem... I assumed that in order for the ODE to be zero, that I had to pick x' and y' cleverly so that the two terms canceled out. But, I have another option: I can pick x and y cleverly so that both terms are zero!

Because I tried to pick x' and y' cleverly they both zero out at this particular solution, which means that when I try to take "infinitessimal steps" of size [x', y']^T, I'm not going anywhere. But, now that I've spotted the problem, I can just take the solution for x and y that work, and I've already figured that out from the eigenvector:

[x, y] = t [2, 1]


But I can easily read it off of the equation too, by factoring:

(2x - 4y) y' + (x - 2y) x' = (x - 2y) (2y' + x')

So I just need x - 2y = 0, or y = (1/2) x.


Note that the original equation is not linear, so we cannot just add this to the previously determined solution!

Working it out, we have two families:

[x, y] = (At + B) [2, 1]
and
[x, y] = B [2, 1] + C exp(-4 t) [2, -1]

(Because if you plug in, you discover that AC must be zero)

Stupid quadratic equations.

(You notice that the equation is of the form x^T M dx = 0 for some matrix M?)

 

[saltydog]

Working it out, we have two families:

[x, y] = (At + B) [2, 1]
and
[x, y] = B [2, 1] + C exp(-4 t) [2, -1]

(You notice that the equation is of the form x^T M dx for some matrix M?)

Is the negative exponent a typo? Should it not be positive? Also, I'll spend time with your analysis. Thanks!

 

[Hurkyl]

No, the negative is correct. My parametrization has the opposite orientation!

(Notice our original ODE's are off by a factor of -1)

 

[saltydog]

No, the negative is correct. My parametrization has the opposite orientation!

(Notice our original ODE's are off by a factor of -1)

Thanks for the clairification Hurkyl. I'll spend time with it. Also, I tell you what, this:

\frac{dy}{dt}=Ax+By+E

\frac{dx}{dt}=Cx+Dy+F

should be comprehensively catagorized and I suspect it is somewhere already. That is, what does it do as a function of the parameters? Surely someone has already worked this out. I just don't have the reference.

 

[lurflurf]

Thanks for the clairification Hurkyl. I'll spend time with it. Also, I tell you what, this:

\frac{dy}{dt}=Ax+By+E

\frac{dx}{dt}=Cx+Dy+F

should be comprehensively catagorized and I suspect it is somewhere already. That is, what does it do as a function of the parameters? Surely someone has already worked this out. I just don't have the reference.

matrix form is easier
x'=Ax+b
related homogeneous problem
x'=Ax
solution
x=exp(At)x0
variation of parameters
x=exp(At)u
u'=exp(-At)b
x=e^{At}x_0+e^{At}\int e^{-At}b dt
also undetermined coeficents works well
for b constant
b'=0

 

[asdf1]

wow!
@@a
this is the first time I've seen matrix form used in solving differential equations...

 

[saltydog]

matrix form is easier
x'=Ax+b
related homogeneous problem
x'=Ax
solution
x=exp(At)x0
variation of parameters
x=exp(At)u
u'=exp(-At)b
x=e^{At}x_0+e^{At}\int e^{-At}b dt
also undetermined coeficents works well
for b constant
b'=0

Jesus Lurflurf. Why am I not surprised . . . Can you kindly help me with a matter of notation:

If:

A=\left[\begin{array}{c} ax+by \\<br /> cx+dy<br /> \end{array}\right]<br />

Then what is:

e^{At}

Or if I'm mis-interpreting your notation would you explain a bit further?

 

[qbert]

it's more like
<br /> \left( \begin{array}{c} x&#039;(t) \\ y&#039;(t) \end{array} \right) =<br /> \left[ \begin{array}{cc} a &amp; b \\ c &amp; d \end{array} \right] <br /> \left( \begin{array}{c} x(t) \\ y(t) \end{array} \right) +<br /> \left( \begin{array}{c} b_1 \\ b_2 \end{array} \right) <br />

gives
\mathbf{x&#039;} = \mathbf{Ax + b}

given some matrix A then exp(A) is
I + A + \frac{1}{2!}A^2 + \frac{1}{3!}A^3 + \ldots

which I always thought was a singularly unhelpful way to define anything.

It's a little easier if A is diagonal. Then the elements of Aⁿ
are just a_iiⁿ. That is, if A is diagonal you just
exponentiate along the main diagonal.

example:
<br /> \exp{\left[ \begin{array}{cc} a &amp; 0 \\ 0 &amp; d \end{array} \right] } = <br /> \left[ \begin{array}{cc} e^a &amp; 0 \\ 0 &amp; e^d \end{array} \right] <br />

If you can diagonalize A. (That is if there is some matrix such that
TDT^-1 = A). Then you can get exp(A) fairly easy.
Aⁿ = (TDT^-1) (TDT^-1)...(TDT^-1)
= (TDⁿT^-1)

\exp{A} = I + A + \frac{1}{2!}A^2 + \frac{1}{3!}A^3 + \ldots
= TT^{-1} + TDT^{-1} + \frac{1}{2!}(TDT^{-1})^2 + \frac{1}{3!}(TDT^{-1})^3 + \ldots
= TT^{-1} + TDT^{-1} + (T \frac{1}{2!}D^2T^{-1}) + (T\frac{1}{3!}D^3T^{-1}) + \ldots
= T(I + D + \frac{1}{2!}D^2 + \frac{1}{3!}D^3 + \ldots)<br /> T^{-1}
\exp{A} = Te^DT^{-1}

Of course, it just so happens if you make a matrix whose columns
are the eigenvectors of A you get T. (I'll leave the proof to whomever
is interested.)

If A is invertible and b is constant you can solve the
x' = Ax + b system super easy.
note x' = A(x + A^-1b)
make a linear change of variables
y = x + A^-1b,
then y' = x' and the system
is y' = Ay
whose solution is y = exp(At) c
where c is a column vector of arbitrary constants
and
x = y - A^-1b = exp(At) c - A^-1b

Now the questions comes up, under what
conditions can you diagonalize A? what should
you do if you can't? what if A is not invertible?

etc.

 

[saltydog]

it's more like
<br /> \left( \begin{array}{c} x&#039;(t) \\ y&#039;(t) \end{array} \right) =<br /> \left[ \begin{array}{cc} a &amp; b \\ c &amp; d \end{array} \right] <br /> \left( \begin{array}{c} x(t) \\ y(t) \end{array} \right) +<br /> \left( \begin{array}{c} b_1 \\ b_2 \end{array} \right) <br />

gives
\mathbf{x&#039;} = \mathbf{Ax + b}

given some matrix A then exp(A) is
I + A + \frac{1}{2!}A^2 + \frac{1}{3!}A^3 + \ldots

which I always thought was a singularly unhelpful way to define anything.

It's a little easier if A is diagonal. Then the elements of Aⁿ
are just a_iiⁿ. That is, if A is diagonal you just
exponentiate along the main diagonal.

example:
<br /> \exp{\left[ \begin{array}{cc} a &amp; 0 \\ 0 &amp; d \end{array} \right] } = <br /> \left[ \begin{array}{cc} e^a &amp; 0 \\ 0 &amp; e^d \end{array} \right] <br />

If you can diagonalize A. (That is if there is some matrix such that
TDT^-1 = A). Then you can get exp(A) fairly easy.
Aⁿ = (TDT^-1) (TDT^-1)...(TDT^-1)
= (TDⁿT^-1)

\exp{A} = I + A + \frac{1}{2!}A^2 + \frac{1}{3!}A^3 + \ldots
= TT^{-1} + TDT^{-1} + \frac{1}{2!}(TDT^{-1})^2 + \frac{1}{3!}(TDT^{-1})^3 + \ldots
= TT^{-1} + TDT^{-1} + (T \frac{1}{2!}D^2T^{-1}) + (T\frac{1}{3!}D^3T^{-1}) + \ldots
= T(I + D + \frac{1}{2!}D^2 + \frac{1}{3!}D^3 + \ldots)<br /> T^{-1}
\exp{A} = Te^DT^{-1}

Of course, it just so happens if you make a matrix whose columns
are the eigenvectors of A you get T. (I'll leave the proof to whomever
is interested.)

If A is invertible and b is constant you can solve the
x' = Ax + b system super easy.
note x' = A(x + A^-1b)
make a linear change of variables
y = x + A^-1b,
then y' = x' and the system
is y' = Ay
whose solution is y = exp(At) c
where c is a column vector of arbitrary constants
and
x = y - A^-1b = exp(At) c - A^-1b

Now the questions comes up, under what
conditions can you diagonalize A? what should
you do if you can't? what if A is not invertible?

etc.

Thanks a lot Qbert. I'm not supprised neither but I digress. It's all very interesting to me, and I wish to better obtain a handle on the global dynamics of the system as a whole.

 

[saltydog]

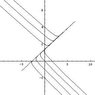
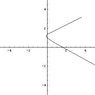
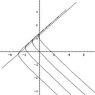
Alright, it's all in my Linear Algebra and DE textbooks. Jesus. I have no excuses. I'll review.

Salty

 

[saltydog]

You know what get's me, we started with:

\frac{dy}{dx}=\frac{-x+2y-3}{2x-4y+5},\quad y(x_0)=y_0

This is (parametrically) equivalent to:

\left(\begin{array}{c} x^{&#039;} \\<br /> y^{&#039;}<br /> \end{array}\right)=<br /> \left(\begin{array}{cc} 2 &amp; -4 \\<br /> -1 &amp; 2<br /> \end{array}\right)<br /> \left(\begin{array}{c} x \\<br /> y<br /> \end{array}\right)+<br /> \left(\begin{array}{c} 5 \\<br /> -3<br /> \end{array}\right);<br /> \quad<br /> \left(\begin{array}{c} x_0 \\<br /> y_0<br /> \end{array}\right)<br />

Now from what I've reviewed thus far, if the determinant of the eigenvectors is non-zero, this is easily solved. Wonderful . . . that's just wonderful . . .

Seem to me that this is by far the best approach to solving this ODE. I'm sure that's what you guys meant up there. No doubt I'd be interested in learning what to do if the eigenvalue determinant is zero but first I'll have to work this one through to completion just to get caught up.

 

[saltydog]

A summary

Asdf, I'm doing this because I want to, it helps me (relearn) it, and I enjoy it and maybe others interested in the details can learn from it. You, well just do whatever you want ok.

\frac{dy}{dx}=\frac{-x+2y-3}{2x-4y+5};\quad y(0)=1

Converting to parametric form:

\frac{dx}{dt}=2x-4y+5;\quad x(0)=0

\frac{dy}{dt}=-x+2y-3;\quad y(0)=1

Expressing this as a non-homogeneous system of equations:

\left(\begin{array}{c}x \\ y \end{array}\right)^{&#039;}=<br /> \left(\begin{array}{cc} 2 &amp; -4 \\<br /> -1 &amp; 2 \end{array}\right)<br /> \left(\begin{array}{c}x \\ y \end{array}\right)+<br /> \left(\begin{array}{c} 5 \\ -3 \end{array}\right);\quad <br /> \left(\begin{array}{c}0 \\ 1 \end{array}\right)<br />

Solving for the eigenvalues and eigenvectors for the homogeneous system we obtain:

\left(\begin{array}{c} x \\ y \end{array}\right)_c=<br /> a_1\left(\begin{array}{c} 2 \\ 1 \end{array}\right)+<br /> a_2\left(\begin{array}{c} -2 \\ 1 \end{array}\right)e^{4t}<br />

Employing variation of parameter to find a particular solution we let:

\left(\begin{array}{c} x \\ y \end{array}\right)_p=<br /> a_1(t)\left(\begin{array}{c} 2 \\ 1 \end{array}\right)+<br /> a_2(t)\left(\begin{array}{c} -2 \\ 1 \end{array}\right)e^{4t<br />

Substituting this expression into the non-homogeneous system above and noting that the complimentary solution satisfies the system, results in:

a_1^{&#039;}(t)\left(\begin{array}{c} 2 \\ 1 \end{array}\right)+<br /> a_2^{&#039;}(t)\left(\begin{array}{c} -2 \\ 1 \end{array}\right)e^{4t}=<br /> \left(\begin{array}{c} 5 \\ -3 \end{array}\right)<br />

or:

\left(\begin{array}{cc} 2 &amp; -2 \\<br /> 1 &amp; 1 \end{array}\right)<br /> \left(\begin{array}{c} a_1^{&#039;}(t) \\<br /> a_2^{&#039;}(t)e^{4t} \end{array}\right)=<br /> \left(\begin{array}{c} 5 \\ -3 \end{array}\right)<br />

Now, if the determinant is not zero, this is easily solved for a_1^{&#039;}[/tex] and a_2^{&amp;#039;}[/tex] via Cramer&amp;#039;s rule.&lt;br /&gt; &lt;br /&gt; We find:&lt;br /&gt; &lt;br /&gt; a_1^{&amp;amp;#039;}(t)=-1/4&lt;br /&gt; &lt;br /&gt; a_2^{&amp;amp;#039;}(t)=-11/4e^{-4t}&lt;br /&gt; &lt;br /&gt; Integrating:&lt;br /&gt; &lt;br /&gt; a_1(t)=-1/4t&lt;br /&gt; &lt;br /&gt; a_2(t)=11/16e^{-4t}&lt;br /&gt; &lt;br /&gt; Thus the particular solution is:&lt;br /&gt; &lt;br /&gt; \left(\begin{array}{c} x \\ y \end{array}\right)_p=&amp;lt;br /&amp;gt; -\frac{1}{4}t\left(\begin{array}{c} 2 \\ 1 \end{array}\right)+&amp;lt;br /&amp;gt; 11/16\left(\begin{array}{c} -2 \\ 1 \end{array}\right)&amp;lt;br /&amp;gt;&lt;br /&gt; &lt;br /&gt; and therefore the general solution is:&lt;br /&gt; &lt;br /&gt; \left(\begin{array}{c} x \\ y \end{array}\right)_g=&amp;lt;br /&amp;gt; -\frac{1}{4}t\left(\begin{array}{c} 2 \\ 1 \end{array}\right)+&amp;lt;br /&amp;gt; 11/16\left(\begin{array}{c} -2 \\ 1 \end{array}\right)+&amp;lt;br /&amp;gt; a_1\left(\begin{array}{c} 2 \\ 1 \end{array}\right)+&amp;lt;br /&amp;gt; a_2\left(\begin{array}{c} -2 \\ 1 \end{array}\right)e^{4t&amp;lt;br /&amp;gt;&lt;br /&gt; &lt;br /&gt; where a_1 anda_2 are now arbitrary constants.&lt;br /&gt; Finally, solving for the initial conditions:&lt;br /&gt; &lt;br /&gt; \left(\begin{array}{c}0 \\ 1 \end{array}\right)=&amp;lt;br /&amp;gt; \left(\begin{array}{c} -22/16 \\&amp;lt;br /&amp;gt; 11/16 \end{array}\right)+&amp;lt;br /&amp;gt; a_1\left(\begin{array}{c} 2 \\ 1 \end{array}\right)+&amp;lt;br /&amp;gt; a_2\left(\begin{array}{c} -2 \\ 1 \end{array}\right)&amp;lt;br /&amp;gt;&lt;br /&gt; &lt;br /&gt; Solving for a_1 and a_2 and substituting into the general solution, we obtain the same answer as above:&lt;br /&gt; &lt;br /&gt; x(t)=-3/8-\frac{1}{2}t+3/8e^{4t}&lt;br /&gt; &lt;br /&gt; y(t)=19/16-\frac{1}{4}t-3/16e^{4t}&lt;br /&gt; &lt;br /&gt; Oh yea, thanks Hurkyl, lurflurf, and qbert &lt;img src=&quot;https://cdn.jsdelivr.net/joypixels/assets/8.0/png/unicode/64/1f642.png&quot; class=&quot;smilie smilie--emoji&quot; loading=&quot;lazy&quot; width=&quot;64&quot; height=&quot;64&quot; alt=&quot;:smile:&quot; title=&quot;Smile :smile:&quot; data-smilie=&quot;1&quot;data-shortname=&quot;:smile:&quot; /&gt; .

 

[asdf1]

@@a
jeepers!
i've got to get out my mathematical physics textbook out and review it too~
thanks! :)

 

[saltydog]

For the record I wish to document a fourth means of solving this equation by means of Laplace Transforms:

For the system:

\frac{dx}{dt}=2x-4y+5;\quad x(0)=0

\frac{dy}{dt}=-x+2y-3;\quad y(0)=1

Letting:

\mathcal{L}\{x(t)\}=u(s)

\mathcal{L}\{y(t)\}=v(s)

and taking the Laplace Transform of both sides of both equations we obtain the algebraic system of equations:

su=2u-4v+5/s

sv-1=-u+2v-3/s

Solving for u and v:

u=-\frac{s+2}{(s-4)s^2}

v=\frac{1-5s+s^s}{(s-4)s^2}

Upon taking the Inverse Laplace Transforms of these expressions, we once again obtain the same formulas for x(t) and y(t) as above:

x(t)=-3/8-\frac{1}{2}t+3/8 e^{4t}

y(t)=19/16-\frac{1}{4}t-3/16e^{4t}

 

[saltydog]

I just realized something: For this problem and the other one Asdf posted, the solution, using Laplace Transforms, can be obtained in three easy steps in Mathematica:

alist = {u, v} /. 
    Solve[{s u == 2 u - 4 v + 5/s, s v - 1 == - u + 2 v - 3/s}, {u, v}]
x = InverseLaplaceTransform[alist[[1, 1]], s, t]
y = InverseLaplaceTransform[alist[[1, 2]], s, t]

I find that amazing! Granted, in general, I'd have to include two extra lines to first calculate the transform and this doesn't help one learn the math; I would not recommend this to anyone just learning the technique, but once learned, this provides an effective, concise means of approching the global behavior of these systems.