prof chaos
- 2
- 0
Sorry if I'm doing this wrong... first time poster.
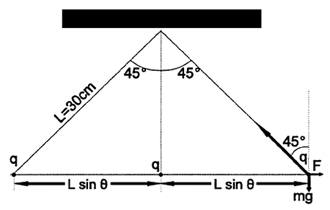
The diagram gives the relevant info. All three q's are equal point charges of m=0.10 kg. I'm trying to find the value of q.
Coulombs law and basic trig.
Considering either of the outer point charges, I have thus figured out that F_x=Tsinθ and mg=Tcosθ. Dividing those gives F=mgTanθ=0.98N
I can't figure out what to do at all for the second part where I use Coulombs law to combine the the forces of both charges on the most right one. My prof gave the following HW explanation, but I don't understand it:
\frac{Kq^2}{(Lsin\Theta)^2} -- \frac{kq^2}{(2Lsin\Theta)^2} = \frac{5kq^2}{4L^2(sin^2)\Theta}
I can rearrange and solve from there... I understand where \frac{Kq^2}{(Lsin\Theta)^2} -- \frac{kq^2}{(2Lsin\Theta)^2} comes from but how in the world does that turn into \frac{5kq^2}{4L^2(sin^2)\Theta}
Ugh it turned my thetas into 952;... I hope you still understand it.
Homework Statement
The diagram gives the relevant info. All three q's are equal point charges of m=0.10 kg. I'm trying to find the value of q.
Homework Equations
Coulombs law and basic trig.
The Attempt at a Solution
Considering either of the outer point charges, I have thus figured out that F_x=Tsinθ and mg=Tcosθ. Dividing those gives F=mgTanθ=0.98N
I can't figure out what to do at all for the second part where I use Coulombs law to combine the the forces of both charges on the most right one. My prof gave the following HW explanation, but I don't understand it:
\frac{Kq^2}{(Lsin\Theta)^2} -- \frac{kq^2}{(2Lsin\Theta)^2} = \frac{5kq^2}{4L^2(sin^2)\Theta}
I can rearrange and solve from there... I understand where \frac{Kq^2}{(Lsin\Theta)^2} -- \frac{kq^2}{(2Lsin\Theta)^2} comes from but how in the world does that turn into \frac{5kq^2}{4L^2(sin^2)\Theta}
Ugh it turned my thetas into 952;... I hope you still understand it.