Solving Double Integral with Polar Coordinates

[asmani]

Hi all.

Suppose that we want to compute the following indefinite integral:

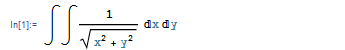
The correct solution by Mathematica:

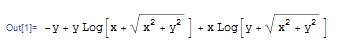
Now here is the (apparently) incorrect solution by using polar coordinates:
\iint\frac{1}{\sqrt{x^2+y^2}}dxdy=\iint\frac{1}{r}rdrd\theta=(r+c_1)(\theta+c_2)
If c₁=c₂=0, then one solution is:
r\theta=\sqrt{x^2+y^2}\tan^{-1}\left ( \frac{y}{x} \right )
But it isn't:

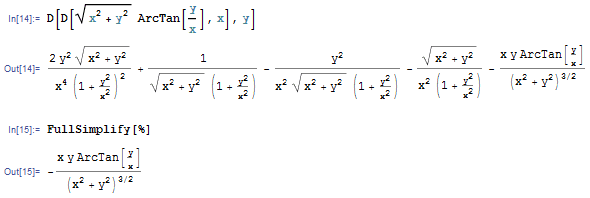
What's wrong with this solution?

Thanks in advance.

 

[AdrianMay]

$\iint\frac{1}{r}rdrd\theta$ looks good to me but that would just be $\iint drd\theta$ with $0<r<\infty$ and $0<\theta<2\pi$ which is $\infty$. I was already worried about that when I saw the pole at the origin but apparently you can fix it by chopping the radius of interest.