mr bob
- 38
- 0
Just come across a question and I'm at a point where i see no further.
A uniform rod AB, of mass m and length 2a, is free to rotate in a vertical plane, about the end A. A light elastic string of modulus kmg and natural length a, has one and attached to B and the other end to a fixed point O which is vertically above A with OA = 2a. Show that when AB makes an angle \theta with the downward vertical, the potential energy, V, of the system when the string is stretched is given byV = mga[(4k - 1)\cos\theta -4k\cos\frac{\theta}{2}] + constant
I drew the following diagram:-
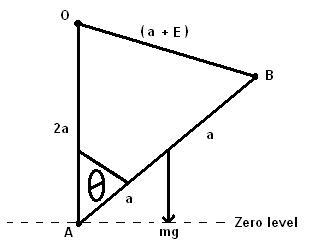
I equated the GPE of the uniform rod to be
AB = -mg\cos\theta
And when it comes to calculating the energy of the elastic string i tried:
OC = \frac{\lambda x^2}{2a}
Where x is the extension in the string, which i calculated to be:
x = (2a\sin\theta - a)
So:
OB = \frac{kmg(2a\sin\theta - a)^2}{2a}
OB = \frac{kmga(4\sin^2\theta -4\sin\theta + 1)}{2}
OB = 2kmgasin^2\theta -2kmg\sin\theta + \frac{kmg}{2}
But since:
OB = \frac{kmg}{2} is a constant, we can take it out of the equation.
Using the identity: \sin^2\theta = 2\sin\theta\cos\theta
4kmga\sin\theta\cos\theta -2kmga\sin\theta
However i can't get the 2nd term in the above equation to equal 4kmga\cos\frac{\theta}{2}
Any help would be really appreciated.
Thank you.
A uniform rod AB, of mass m and length 2a, is free to rotate in a vertical plane, about the end A. A light elastic string of modulus kmg and natural length a, has one and attached to B and the other end to a fixed point O which is vertically above A with OA = 2a. Show that when AB makes an angle \theta with the downward vertical, the potential energy, V, of the system when the string is stretched is given byV = mga[(4k - 1)\cos\theta -4k\cos\frac{\theta}{2}] + constant
I drew the following diagram:-
I equated the GPE of the uniform rod to be
AB = -mg\cos\theta
And when it comes to calculating the energy of the elastic string i tried:
OC = \frac{\lambda x^2}{2a}
Where x is the extension in the string, which i calculated to be:
x = (2a\sin\theta - a)
So:
OB = \frac{kmg(2a\sin\theta - a)^2}{2a}
OB = \frac{kmga(4\sin^2\theta -4\sin\theta + 1)}{2}
OB = 2kmgasin^2\theta -2kmg\sin\theta + \frac{kmg}{2}
But since:
OB = \frac{kmg}{2} is a constant, we can take it out of the equation.
Using the identity: \sin^2\theta = 2\sin\theta\cos\theta
4kmga\sin\theta\cos\theta -2kmga\sin\theta
However i can't get the 2nd term in the above equation to equal 4kmga\cos\frac{\theta}{2}
Any help would be really appreciated.
Thank you.
Last edited: