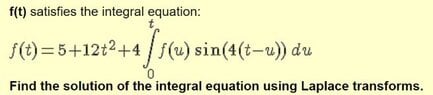Solving Integral Equation w/ Laplace Transform - Abdullah

[Prove It]

View attachment 9669

We would need to recognise that the integral in the equation is a convolution integral, which has Laplace Transform: $\displaystyle \mathcal{L}\,\left\{ \int_0^t{ f\left( u \right) \,g\left( t - u \right) \,\mathrm{d}u } \right\} = F\left( s \right) \,G\left( s \right) $.

In this case, $\displaystyle g\left( t - u \right) = \sin{ \left[ 4\left( t - u \right) \right] } \implies g\left( t \right) = \sin{ \left( 4\,t \right) } \implies G\left( s \right) = \frac{4}{s^2 + 16} $.

Taking the Laplace Transform of the equation gives

$\displaystyle \begin{align*} F\left( s \right) &= 5 \left( \frac{1}{s} \right) + 12 \left( \frac{2}{s^3} \right) + 4\,F\left( s \right) \left( \frac{4}{s^2 + 16} \right) \\
F\left( s \right) &= \frac{5}{s} + \frac{24}{s^3} + \left( \frac{16}{s^2 + 16} \right) F\left( s \right) \\
F\left( s \right) - \left( \frac{16}{s^2 + 16} \right) F\left( s \right) &= \frac{5}{s} + \frac{24}{s^3} \\
\left( 1 - \frac{16}{s^2 + 16} \right) F\left( s \right) &= \frac{5}{s} + \frac{24}{s^3} \\
\left( \frac{s^2}{s^2 + 16} \right) F\left( s \right) &= \frac{5\,s^2 + 24}{s^3} \\
F\left( s \right) &= \frac{\left( s^2 + 16 \right) \left( 5\,s^2 + 24 \right) }{s^5} \\
F\left( s \right) &= \frac{5\,s^4 + 104\,s^2 + 384}{s^5} \\
F\left( s \right) &= \frac{5}{s} + \frac{104}{s^3} + \frac{384}{s^5} \\
F\left( s \right) &= 5\left( \frac{1}{s} \right) + 52 \left( \frac{2}{s^3} \right) + 16 \left( \frac{4!}{s^5} \right) \\
\\
f\left( t \right) &= 5 + 52\,t^2 + 16\,t^4
\end{align*} $

 

[jvicens]

I would like to point out that the Laplace Transform is a powerful tool in solving differential equations and finding solutions to complex mathematical problems. In this case, the Laplace Transform of the convolution integral helps us to find the function $f(t)$ that satisfies the given equation. This method is widely used in various fields of science and engineering, such as signal processing, control systems, and quantum mechanics. It is important to understand and utilize the Laplace Transform in order to solve real-world problems and advance our understanding of the physical world.