Discussion Overview
The discussion revolves around solving magnetic torque problems using unit vectors, specifically in the context of a homework assignment. Participants explore the calculation of magnetic moment and torque, the application of the right-hand rule, and the resolution of vectors into components.
Discussion Character
- Homework-related
- Technical explanation
- Conceptual clarification
- Debate/contested
Main Points Raised
- One participant states the formula for magnetic moment as m=N*I*A and expresses confusion about computing the unit vector.
- Another participant suggests using the magnitude of the cross product for torque, indicating it may be a quicker approach than determining unit vectors.
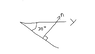
- There is a discussion about the angle between the magnetic moment and magnetic field, with one participant asserting it is 60 degrees and seeking clarification on applying this to the torque vector.
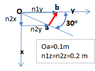
- Another participant emphasizes the need to find the components of the unit vector and describes a method for calculating it based on the difference between two end vectors.
- Several participants discuss how to resolve the unit vector into x and y components, with suggestions to improve the drawing for clarity and to use a magnitude of 1 for the unit vector.
- One participant notes that the difference in unit vectors is independent of the choice of origin, suggesting a simplification for the algebra involved.
Areas of Agreement / Disagreement
Participants express varying levels of understanding regarding the calculation of unit vectors and the application of the right-hand rule. While some agree on the angle between the magnetic moment and magnetic field being 60 degrees, the method for defining the magnetic moment in terms of x and y components remains a point of confusion and discussion.
Contextual Notes
Participants have not reached a consensus on the best approach to define the magnetic moment in terms of its components, and there are unresolved questions about the application of the cross product in this context.