Solving Magnetism Question: What Current & Direction is Needed?

[adwlacrosse75]

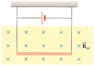
A conductor suspended by two flexible wires as shown in Figure P19.18 has a mass per unit length of 0.0500 kg/m.

Figure P19.18 (The picture is an attachment)

What current must exist in the conductor for the tension in the supporting wires to be zero when the magnetic field is 3.70 T into the page?

What is the required direction for the current?

Thanks a lot guys I'm new to the board and looking for some help. I appreciate it!

 

[Doc Al]

What have you done so far?

How do you find the magnetic force on a current-carrying wire?

 

[adwlacrosse75]

Magnetic force on a current carrying conductor/wire

F=B(magnetic field)I(Current)L(Length)sin(theta)

I have no idea where to start can you help me out here or just get me started.

Whats throwing me off is this mass per unit length and the tension

 

[Doc Al]

Whats throwing me off is this mass per unit length and the tension

The mass per unit length will help you find the weight of the conductor.

In order for there to be zero tension in the support wires, what must the net force be on the conductor?

 

[adwlacrosse75]

well for there to be zero tension in the support wires the net force should just be the opposite of the weight just like a bouyant force on a floating object. But if I don't have a length how can i get the weight of the object. I think that's the exact thing that's screwing me up.

 

[Doc Al]

well for there to be zero tension in the support wires the net force should just be the opposite of the weight just like a bouyant force on a floating object.

That's not exactly right. (I think you're on the right track--you're just describing it incorrectly.) What two forces act on the conductor?

But if I don't have a length how can i get the weight of the object. I think that's the exact thing that's screwing me up.

Maybe you don't need an actual value. Hint: Just call the length L and see what happens.