Solving Motion of m w/ Respect to O: Spring & Damper

[bobred]

Homework Statement

I am asked to write down the equation of motion of m with respect to O, hence show that x(t) satisfies the differential equation.

m\ddot{x}+r\dot{x}+kx=mg+kl_0+m\ddot{y}

See attached diagram.

Homework Equations

I have the force of the spring H, the Damping R and the weight W as

\bold{H}=k(x-y-l_0)\bold{i}
\bold{R}=r\dot{x}\bold{i}
\bold{W}=-mg\bold{i}

The Attempt at a Solution

Using the above forces and \bold{F}=m\ddot{x}, what I get is
m\ddot{x}-r\dot{x}-kx=-mg-kl_0-ky

Do I have the forces H, R and W correct, if so how how do I get

m\ddot{x}+r\dot{x}+kx=mg+kl_0+m\ddot{y} ?

Thanks, James

 

[collinsmark]

[Edit: comments deleted. I might have made a mistake with my advice; I'd like to review original post. It's been awhile since I've done this type of mechanics before, and I don't want to mislead the original poster. I'll follow up with a new post shortly. ]

 

[collinsmark]

[Okay, I've totally redone the problem for myself, and I'm glad I did. I made a couple of critical mistakes in my first reply. If you happened to have read the first reply, just ignore it (and sorry ). I'm fairly confident now my advice should much better in this post.]

Hello James,

Let me attempt to get you going. A couple of things first:

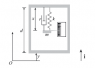
(1) Forces pointing up (in the positive i direction) are positive. But be careful when dealing with x, due to the way it is defined in the figure. If x increases, it means the mass moves down, not up. So when dealing with x specifically, things like displacement, velocity and acceleration, terms involving x need a negative sign attached if they are in the up direction. (y is different than x in this respect. With y, positive means up.)

(2) I'm assuming that l_0 is the length of the spring when it is not stretched.

(3) There might be more that one way to approach this problem. I'm going to make an effort to keep everything in the inertial frame O. But you might be able to work the problem differently if you use an accelerating frame as your reference (but should give you the same answers, since we're not dealing with relativity). But since the problem statement said to keep things in terms of O, that's what I'm attempting to do (O is not accelerating).

\bold{H}=k(x-y-l_0)\bold{i}

Something is not right with the above. Why should the force from the spring be a function of y? Allow me to explain. Suppose everything is in equilibrium. Now imagine slowly lifting the whole contraption up to the ceiling, such that it is again in equilibrium. The force from the spring doesn't change, even though y is much larger now. So the force from the spring shouldn't depend on y.

\bold{R}=r\dot{x}\bold{i}

Looks okay to me.

\bold{W}=-mg\bold{i}

That also looks okay. On a side note, if you were to solve this problem in terms of an accelerating reference frame, above is where you would insert some sort of m \ddot{y} term (instead of where I recommend putting it [see below]). But since we're not working with accelerated frames (well, at least I'm not in this post), it doesn't belong there. So your W looks fine to me the way it is.

Okay so now there is one final part: the resultant force. This is the sum of all the other forces involved on the mass m. Newton's second law states that ma = F_net. You can calculate F_net easily enough by summing all the above forces. But what actually is a, really?

All the F_net related forces are in respective to the box. But what if we move the box? What if pick up the box and start shaking it? Move it back and forth? Or drop-kick the thing? We need to find the acceleration relative to O, not the box itself!

So what is the acceleration of m relative to O? It's the acceleration of m relative to the box, plus the acceleration of the whole box relative to O!

So a is going to be some sort of combination of both \ddot{y} and \ddot{x}. (Hint: remember, be careful of the sign whenever you deal with an x term, as I mentioned before.)

Good Luck!

 

[bobred]

Thank you, here we go

\bold{H}=k(x-l_0)\bold{i}
\bold{R}=r\dot{x}\bold{i}
\bold{W}=-mg\bold{i}

giving the equation of motion

m\ddot{x}=-mg+r\dot{x}+kx-kl_0

So the acceleration is a combination of accelerations of m relative to the box and to O, so we have

m(\ddot{y}-\ddot{x})=-mg+r\dot{x}+kx-kl_0, as said the extn of x is in the negative i direction and y in the positive, giving
-\ddot{x}-r\dot{x}-kx=-mg-kl_0-m\ddot{y} the multiply both sides by -1
\ddot{x}+r\dot{x}+kx=mg+kl_0+m\ddot{y}

I had come to this equation earlier, but wasn't sure how I got there. Thank you for your help and especially the explanations of why!

Thanks, James

 

[bobred]

Hi

I have completed the questions apart from this one

The instrument measures the displacement z from the equilibrium position, z=x-x_{eq}. Find the differential eqn satisfied by z.

Am I right in thinking I should replace x with z+x_{eq} in the eqn of motion

\ddot{x}+r\dot{x}+kx=mg+kl_0+m\ddot{y}

Thanks, James

 

[collinsmark]

Hello James,

I think you forgot an m in your \ddot{x} term. Other than that, your equation looks good.

Hi

I have completed the questions apart from this one

The instrument measures the displacement z from the equilibrium position, z=x-x_{eq}. Find the differential eqn satisfied by z.

Am I right in thinking I should replace x with z+x_{eq} in the eqn of motion

\ddot{x}+r\dot{x}+kx=mg+kl_0+m\ddot{y}

Thanks, James

Sounds reasonable to me. Just remember that when calculating \dot{z} and \ddot{z} that x_{eq} is a constant. It makes a difference. The final differential equation shouldn't have any x's or its derivatives left in it (there will be one x_{eq} though).

 

[bobred]

Hi

Yeah I left out the m term.

Again thank you for your help.

James