- #1
spookyfw
- 25
- 0
Hey all,
some weeks ago in a tutorial our TA solved Poissons equation with Greens functions..would be very short, but he also derived the Greens function using a Fourier transform. Two points I really don't get and he could also not explain it. Maybe you can help me? There might be even a short way..but if you could help out here and tell me what went wrong I would be really helpful :)!
Function to solve:
[itex]\nabla^2[/itex] [itex]\Phi[/itex] = -[itex]\frac{\rho}{\epsilon}[/itex] = f(x) = [itex]\nabla^2[/itex] u(x)
Having the Green's function:
[itex]\nabla^2[/itex] G(r,r') = [itex]\delta[/itex](r-r')
[itex]\nabla^2[/itex] G(x) = [itex]\delta[/itex](x)
taking the Fourier transform:
∫[itex]\nabla^2[/itex] G(x)exp(-ikx)dV = 1
and now the big mess is starting: using Greens first identity, namely:
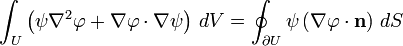
∫[itex]\nabla*\nabla[/itex]G exp(-ikx)dV = ∫[itex]\nabla[/itex] G exp(-ikx) dS - ∫[itex]\nabla[/itex]G [itex]\nabla[/itex] exp(-ikx)dV
then he states that the surface term is equal to zero. I understand that using the Fourier transform we integrate from minus to plus infinity and that we have the condition that our Greens function is usually prone to go to zero at infinity, but how is he doing that step? A integration by parts?
From that he is then coming to the point that
∫G Δexp(-ikx) dV = k^2 ∫ G(r) exp(-ikx) dV
After a substitution he then concludes that G(k) = 1/k^2
To be honest...after applying Greens identity i am somewhat lost. And don't see the steps anymore ;(.Maybe I copied something wrong from the blackboard..it is just driving me nuts!
In the end when transforming back he actually integrates from zero to inf
∫sinc(u) du = pi/2
I always thought this is not possible...that the integral of sinc cannot be given analytically?
As you might have guessed..it is a big constrution site for me...would be very happy if someone could help me out!
some weeks ago in a tutorial our TA solved Poissons equation with Greens functions..would be very short, but he also derived the Greens function using a Fourier transform. Two points I really don't get and he could also not explain it. Maybe you can help me? There might be even a short way..but if you could help out here and tell me what went wrong I would be really helpful :)!
Function to solve:
[itex]\nabla^2[/itex] [itex]\Phi[/itex] = -[itex]\frac{\rho}{\epsilon}[/itex] = f(x) = [itex]\nabla^2[/itex] u(x)
Having the Green's function:
[itex]\nabla^2[/itex] G(r,r') = [itex]\delta[/itex](r-r')
[itex]\nabla^2[/itex] G(x) = [itex]\delta[/itex](x)
taking the Fourier transform:
∫[itex]\nabla^2[/itex] G(x)exp(-ikx)dV = 1
and now the big mess is starting: using Greens first identity, namely:
∫[itex]\nabla*\nabla[/itex]G exp(-ikx)dV = ∫[itex]\nabla[/itex] G exp(-ikx) dS - ∫[itex]\nabla[/itex]G [itex]\nabla[/itex] exp(-ikx)dV
then he states that the surface term is equal to zero. I understand that using the Fourier transform we integrate from minus to plus infinity and that we have the condition that our Greens function is usually prone to go to zero at infinity, but how is he doing that step? A integration by parts?
From that he is then coming to the point that
∫G Δexp(-ikx) dV = k^2 ∫ G(r) exp(-ikx) dV
After a substitution he then concludes that G(k) = 1/k^2
To be honest...after applying Greens identity i am somewhat lost. And don't see the steps anymore ;(.Maybe I copied something wrong from the blackboard..it is just driving me nuts!
In the end when transforming back he actually integrates from zero to inf
∫sinc(u) du = pi/2
I always thought this is not possible...that the integral of sinc cannot be given analytically?
As you might have guessed..it is a big constrution site for me...would be very happy if someone could help me out!