pavadrin
- 154
- 0
Hi
I am having difficulties with another problem involving radian measure.
The problem is as follows:
A wheel of radius 60cm is rotated until a point on the wheel was initially at the lowest point is 80 cm higher than the initial point.
Find a) the angle in radians through which the wheel is rotated
b) the length of the circular path traveled by the point
--------------------------------------------------------------------------
My working for the first part of the problem (a) is as follows:
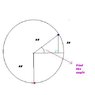
I have drawn the following diagram to assist with my calculations:
https://www.physicsforums.com/attachments/6922
I noe that in a circle there are 2pi radians, therefore in a right angle there are pi/2 radians
I know that at pi/2 radians the point initally at the bottom of the wheel is now 60cm higher, however this is 20cm short of the answer i need. To try and solve this i drew a traingle, however I only know one value of it, so I am unaware on how to find another value.
This piont is where i am lost
Once i how found this value, I can easily contiue the second part of the problem by using this formula: arc length = rӨ where r is the radius of the circle and Ө is the angle measured in radians.
Is my approach to this problem correct? If so, or of incorrect could i please be given a hint on how to continue or the correct method of approach.
Thank you in advance
Pavdarin
I am having difficulties with another problem involving radian measure.
The problem is as follows:
A wheel of radius 60cm is rotated until a point on the wheel was initially at the lowest point is 80 cm higher than the initial point.
Find a) the angle in radians through which the wheel is rotated
b) the length of the circular path traveled by the point
--------------------------------------------------------------------------
My working for the first part of the problem (a) is as follows:
I have drawn the following diagram to assist with my calculations:
https://www.physicsforums.com/attachments/6922
I noe that in a circle there are 2pi radians, therefore in a right angle there are pi/2 radians
I know that at pi/2 radians the point initally at the bottom of the wheel is now 60cm higher, however this is 20cm short of the answer i need. To try and solve this i drew a traingle, however I only know one value of it, so I am unaware on how to find another value.
This piont is where i am lost
Once i how found this value, I can easily contiue the second part of the problem by using this formula: arc length = rӨ where r is the radius of the circle and Ө is the angle measured in radians.
Is my approach to this problem correct? If so, or of incorrect could i please be given a hint on how to continue or the correct method of approach.
Thank you in advance
Pavdarin