Solving Relative Velocity Homework: Man Swimming in River

[Angello90]

Homework Statement

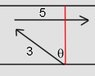
Man can swim 3m/s in the water, water flows 5m/s. River is 176 m wide Find direction at which a) he will end up as little downstream as possible, b) as quick as possible.


2. The attempt at a solution

For b) I think it would be the fastest speed possible i.e. 90 degrees towards bank.
u_r = 5i +0j
u_m = 0i+3j
vm/r = 5i - 3j = 5.83 m/s, which seems to me give the fastest time of 30 seconds.

For a) I'm not too sure, I though the angle would be 45 degrees up stream but than when I work out everything, distance in downstream would be over 200, where in the case of b) downstream was only 170.

Thanks for any hi

 

[HallsofIvy]

Draw a picture. Draw an arrow pointing upward at angle [math]\theta[/math] having length 3t, where t is the time to swim across, to the other bank, then an arrow pointing directly downstream having length 5t m/s . To go "end up downstream as little as possible", the least possible would be no downstream at all which is why I said "to the other bank".

We now have a right triangle with legs of length 3t and 5t and hypotenuse 176 m. The angle upstream is given by $tan(\theta)= \frac{5t}{3t}= \frac{5}{3}$

 

[Angello90]

But this would look like this

Which makes an angle of θ = Sin^-1 5/3, which is impossible.

Why do you take is as Tan θ