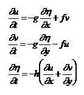groovayness
- 6
- 0
someone please help
The shallow water equations are used to describe, among other things, wave motion in coastal areas, and tidal motions (even across the entire globe, when suitably modified to account for the Earth's spherical geometry). As discussed in class these equations are
(attachment 1)
Eta is the local height of fluid above the equilibrium depth, h.
Show that the expressions for eta, u, and v, below, solve the shallow water equations when the wave speed, omega/k, is (gh)1/2. This is called a Kelvin wave.
(attachment 2)
The shallow water equations are used to describe, among other things, wave motion in coastal areas, and tidal motions (even across the entire globe, when suitably modified to account for the Earth's spherical geometry). As discussed in class these equations are
(attachment 1)
Eta is the local height of fluid above the equilibrium depth, h.
Show that the expressions for eta, u, and v, below, solve the shallow water equations when the wave speed, omega/k, is (gh)1/2. This is called a Kelvin wave.
(attachment 2)