jjmont17
- 1
- 0
So we took a quiz in class, no one got it right so now its take home and I am lost.

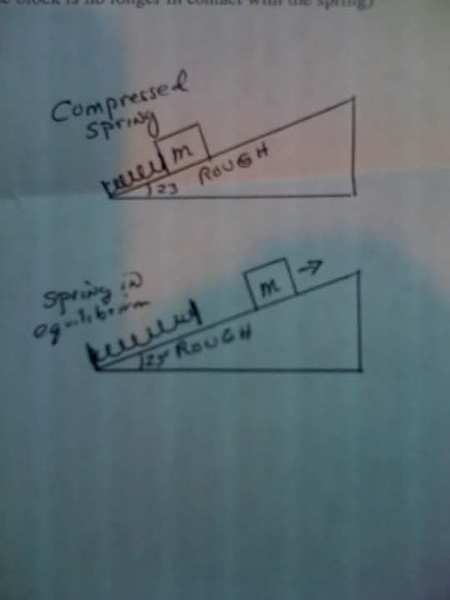
.5kxi -Fkd= .5MVf^2
h=dsin(tht)
umgh=fk
fk=ukN
I really do not know where to start i tried
(1/2)(500n/m)(12.0)-(3.25)(500n/m)(d)=.5(2)(vf^2)
Homework Statement
Homework Equations
.5kxi -Fkd= .5MVf^2
h=dsin(tht)
umgh=fk
fk=ukN
The Attempt at a Solution
I really do not know where to start i tried
(1/2)(500n/m)(12.0)-(3.25)(500n/m)(d)=.5(2)(vf^2)