Solving the Bullet-Block Impulse Problem

[VSCCEGR]

Problem:

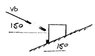
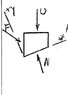
A 20-g bullet is fired into a 4-kg block and becomes embeded in it. knowing that the bullet and block then move up the incline for 1.2 seconds before coming to a stop Determine; (a) the Magnitude Of the bullets initial velocity, (b) the Magnitude of the Impulsive force by the bullet on the block.

Vb_1=? mk=4kg t=1.2s
mb=.02kg

I want to use the Princ. Impulse n' Momentum.
I have tried:
sum(mv_1)=sum(mv_2) but this does not help much

I have also thought of using some sort of constant Accel. Eq. Again to no avail.

Send me in the right direction.

 

[vincentchan]

use the conservation of momentum along the incline plane...

here are some hints:
what is the magnitude of v_0 along the incline plane?
what is the initial velocity of the block? (conservation of momentum)
after you have the initial velocity, the rest should be easy

 

[VSCCEGR]

V_o along the incline is (V_o/2)
Initial Vel. Of block is 0
But how does this apply?

Impulse & Momentum:
sum(mv_1)+sum(Imp_1,2)=sum(mv_2)
Right, So:
sum(mv_1)=mass bullet *v_o
sum(Imp_1,2)=.5F-sin(15)4kg*9.81m/s
sum(mv_2)=(mass bullet+mass block)*v_2

F being the force exerted by the bullet on the block
v_o being velocity of the bullet
v_2 being velocity of bullet and block

F is what is asked for in (b) part
but i need v_o first

 

[Doc Al]

V_o along the incline is (V_o/2)
Initial Vel. Of block is 0

V_0 along the incline (if I read your diagram correctly) is V_0 \cos{30}.

I would treat the problem in two steps:

(1) The collision of bullet and block: The collision is governed by conservation of momentum parallel to the incline.
(2) The slide up the incline: Assuming no friction, the "bullet + block" system starts with some intial speed and has an acceleration down the plane due to gravity.

Do part 2 first.

Since you are not given the time it takes for the bullet to imbed itself into the block, I don't see how you can calculate the impulsive force.

 

[VSCCEGR]

Since you are not given the time it takes for the bullet to imbed itself into the block, I don't see how you can calculate the impulsive force.

Thats what I thought.

So:
V_0=?
V=0
a=9.81m/s verticly or 2.54m/s down incline
m=4.02kg
t=1.2s

cos(30)V_o=velocity of the bullet slong incline

 

[Doc Al]

So:
V_0=?
V=0
a=9.81m/s verticly or 2.54m/s down incline
m=4.02kg
t=1.2s

Use the acceleration and time to solve for the initial speed of the system (post collision) using kinematics. (That's what I called part 2)

 

[ramollari]

As DocAl suggested:

1. Determine the initial post-collision speed of the sytem. You know t, and acceleration (gsin\theta), so find v_0. Then with the law of conservation of momentum determine the magnitude of the bullet's initial velocity.

2. Are you sure that the question doesn't ask for the Impulse J? Or is collision time given?

 

[VSCCEGR]

Found (a):
V=Vo+at
0=Vo+2.54*1.2
Vo=3.04m/s
mv_1=mv_2
.02[V_1/cos(30)]=(4+.02)3.04
V_1=707m/s

as for (b)
i think they mean:
Imp_1,2=F(delta)t
so I am guessing they want to find F(delta)t as a whole using
m_1*v_1+F(delta)t=m_2*v_2

 

[VSCCEGR]

by the way would this problem be done in the same way?

4oz ball @ 9ft/s strikes a 10oz plate on springs with no loss of energy. find Vel. of ball after hitting plate, force exerted by ball on plate.

 

[OlderDan]

Yes, it's the same idea except that in this case you have energy conservation (elastic collision). The ball bounces off the plate. You have the same issue with the force. All you can do is find the total impulse because you cannot know the time or F(t) involved.

 

[ramollari]

as for (b)
i think they mean:
Imp_1,2=F(delta)t
so I am guessing they want to find F(delta)t as a whole using
m_1*v_1+F(delta)t=m_2*v_2

J = \Delta p_{block} = p_{final}

In the final momentum do not add the bullet's mass.

 

[VSCCEGR]

Found (a):
V=Vo+at
0=Vo+2.54*1.2
Vo=3.04m/s
mv_1=mv_2
.02[V_1/cos(30)]=(4+.02)3.04
V_1=707m/s

Sorry ramollari, but you do using this method 707m/s is correct.

 

[OlderDan]

Sorry ramollari, but you do using this method 707m/s is correct.

I think ramollari's comment is directed toward the new problem you asked about, not the original one.

 

[ramollari]

I think ramollari's comment is directed toward the new problem you asked about, not the original one.

No OlderDan, I meant the original problem. Since VSCCEGR was looking for the impulse that the bullet applies on the block, then by definition it is the change of momentum of the block.

J = \Delta p = p_{final} - 0 = p_{final}

 

[OlderDan]

Yes. of course you are right. Same thing applies to both the old problem and the new. I am just getting confused by the sequencing of comments with some of these these add on problems. Thanks for the clarification.