Solving the differential equation of planetary motion

AI Thread Summary
The discussion focuses on a user's attempt to solve the differential equation of planetary motion, noting that their solution does not align with the general solution. They express confusion over why differentiating their result twice does not yield the original equation. The user is familiar with solving methods involving the Complementary Function (CF) and Particular Integral (PI) but seeks clarification on the errors in their approach. Other participants indicate difficulty in understanding the user's equations and suggest a simpler solution might be beneficial. The conversation emphasizes the need for clearer communication and understanding of the differential equation methods used.
RpWinter
Messages
2
Reaction score
0
Hey, this is how i tried solving the differential equation
1Dhki.png

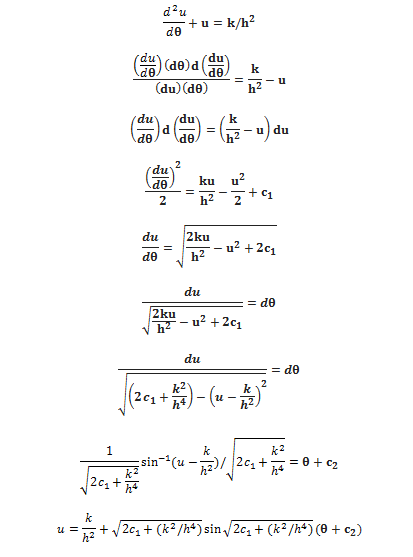
The solution however does not match the general solution of the equation. Also differentiating it twice does not give me the previous equation. Please tell me if i did some mistake while solving.
I already know how to solve by finding CF and PI. I want to know what's wrong with this method.
 

Attachments

  • 1Dhki.png
    1Dhki.png
    6 KB · Views: 3,740
Physics news on Phys.org
dRic2 said:
http://gsjournal.net/Science-Journals/Research Papers-Astrophysics/Download/3763
I have already seen this derivation. Here the differential equation is solved by finding Central function and Particular Integral of the Differential equation. I want to know what's wrong with the method that i have used. Both of them are not giving the same result.
 
Sorry I don't understand your equations or where they came from. I thought you were looking for a simpler solution
 

Thread 'Is calling fictitious forces "not real" just about terminology?'

Hi there, im studying nanoscience at the university in Basel. Today I looked at the topic of intertial and non-inertial reference frames and the existence of fictitious forces. I understand that you call forces real in physics if they appear in interplay. Meaning that a force is real when there is the "actio" partner to the "reactio" partner. If this condition is not satisfied the force is not real. I also understand that if you specifically look at non-inertial reference frames you can...
View full post »

Thread 'Inclined treadmills and Galilean Invariance'

This has been discussed many times on PF, and will likely come up again, so the video might come handy. Previous threads: https://www.physicsforums.com/threads/is-a-treadmill-incline-just-a-marketing-gimmick.937725/ https://www.physicsforums.com/threads/work-done-running-on-an-inclined-treadmill.927825/ https://www.physicsforums.com/threads/how-do-we-calculate-the-energy-we-used-to-do-something.1052162/
View full post »

Thread 'Derivation of Hamilton's Principle: Questions'

I have recently been really interested in the derivation of Hamiltons Principle. On my research I found that with the term ##m \cdot \frac{d}{dt} (\frac{dr}{dt} \cdot \delta r) = 0## (1) one may derivate ##\delta \int (T - V) dt = 0## (2). The derivation itself I understood quiet good, but what I don't understand is where the equation (1) came from, because in my research it was just given and not derived from anywhere. Does anybody know where (1) comes from or why from it the...
View full post »

Similar threads

I Solutions to Simple Harmonic Motion second order differential equation
Replies
1
Views
1K
A Decoupling of a spring mass system
Replies
5
Views
1K
I Making a "Planetary Gear Set" using a 3D printer and PLA material
Replies
4
Views
2K
Learning DEs: Solving 2nd Order Differential Equations
Replies
1
Views
914
Two-body equation of motion resolution
Replies
7
Views
2K
Classical mechanics -- Equations for simulating the motion of a body
Replies
7
Views
1K
I The centripetal acceleration of the planets in our solar system
Replies
19
Views
3K
A Equations of Motion for Torsional Inverted Pendulum on a moving cart
Replies
2
Views
1K
Differential Equation for Projectile Motion with Air Drag
Replies
8
Views
6K
Books on D Operator Method
Replies
5
Views
2K

Hot Threads

Recent Insights

Back
Top