Solving the Uncertainty Principle: Kinetic Energy & Position

[crysien]

I am a little confused by something by something in my physical chemistry textbook.

If two measurable quantities do not commute, then an uncertainty relation exists for them. Kinetic energy and position do not commute, and the expectation value for linear momentum in a 1-D particle in a box is zero. However, the uncertainty relation for KE and position says that:

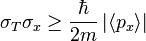
Obviously, the uncertainty can't be zero, but I don't see why this equation is correct and I haven't found anything working out the actual integral to reach this result online. Could someone please explain?

 

[azntoon]

The uncertainty relation for kinetic energy and position states that the product of the uncertainties in these two quantities must be greater than or equal to a certain value. This value is known as the "uncertainty principle" and is equal to h/(4π), where h is Planck's constant. The equation you have given is simply a statement of this principle; it does not imply that the actual values for the uncertainties in these two quantities are zero. In fact, the equations for linear momentum in a 1-D particle in a box only imply that the expectation value for linear momentum is zero, not necessarily the actual value.