Solving Theta Problem o_0: Banking Curved Exit Ramp at 20.125 Radians

[AznBoi]

Homework Statement

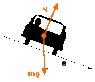
An engineer wishes to design a curved exit ramp for a toll road in such a way that a car will not have to rely on friction to round the curve without skidding. She does so by banking the road in such a way that the force causing the centripetal acceleration will be supplied by the circular path.

a) Show that for a given speed (v) and a radius (r), the curve must be banked at the angle (theta) such that tan \theta= \frac{v^2}{rg}


b) Find the angle at which the curve should be banked if a typical car rounds it at a 50m radius and a speed of 13.4 m/s.

Homework Equations

tan \theta= \frac{v^2}{rg}

The Attempt at a Solution

I have no idea what a) means or how to start it. I know that you have to show it by using the variables given. However, I don't know how you would show it. =P

b) tan \theta= \frac{v^2}{rg}

tan \theta= \frac{13.4m/s^2}{(50m)(9.8m/s^2)}

tan \theta= 0.366449 radians

\theta= tan^{-1}{}0.366449 radians

theta=20.125 radians

Thanks for your help!

 

[gabee]

Try drawing a free-body diagram and listing out the net forces acting on the car, that's always a good idea!

 

[AznBoi]

Try drawing a free-body diagram and listing out the net forces acting on the car, that's always a good idea!

I don't understand the question that well. The road is being tilted to an angle theta right? So that means both the normal force and the centripetal acceleration pointed towards the middle helps with keeping the car in a circular rotation? I don't get how you solve a) though. How are you suppose to show that? Plug numbers in? I'm lost. =/

 

[Zell2]

So that means both the normal force and the centripetal acceleration pointed towards the middle helps with keeping the car in a circular rotation?

The centripetal acceleration isn't a force in itself: a force or a component of a force provides the required centripetal acceleraion.

Try drawing a force diagram as suggested, marking on the two forces acting on the car and then think about what value the components of the unknown force must have.

 

[Hootenanny]

Just to further clarify what Zell2 said; you can think of the centripetal force as "The net force directed towards the centre of the circular motion required to produce the centripetal acceleration".

 

[gabee]

Zell2 is right, a component of one of these forces will provide the centripetal acceleration. Find out which one and set it equal to \frac{mv^2}{r} (centripetal force).

 

[AznBoi]

Zell2 is right, a component of one of these forces will provide the centripetal acceleration. Find out which one and set it equal to \frac{mv^2}{r} (centripetal force).

Well I know that it is the x component of the normal force because the y component and the weight cancel out. So is the x compontent of the normal force pointed parallel to the slope of theta? or does it point horizontally to form a rectanglular box?

 

[AznBoi]

haha nvm. I finally solved a) by using sines and cosines I get it now. So the centripetal force is the net force of the x component of the normal force? Is that why you make them equal to each other?

So in order to find the centripetal acceleration, you divide the net force(centripetal force) by the mass of the object right??

Can someone confirm that part b) is correct? Thanks a lot!

 

[PhanthomJay]

haha nvm. I finally solved a) by using sines and cosines I get it now. So the centripetal force is the net force of the x component of the normal force? Is that why you make them equal to each other? the net force in the x direction, which is the centripetal direction, equals the product of the mass times the acceleration in the x (centripetal) direction, per Newton 2nd Law.[/color]

So in order to find the centripetal acceleration, you divide the net force(centripetal force) by the mass of the object right??yes, which is a_centripetal = v^2/r. The centripetal accceleration is due to a change in direction of the velocity, not a change in its speed.[/color]

Can someone confirm that part b) is correct? Thanks a lot!

Check your units. The tan of an angle has none. The angle itself may be represented in degrees or radians or some other measure. What is the angle?

 

[AznBoi]

Check your units. The tan of an angle has none. The angle itself may be represented in degrees or radians or some other measure. What is the angle?

I think your suppose to find the angle. How come part b) is incorrect? I just plugged all the given numbers into find theta.


Here is b) Find the angle at which the curve should be banked if a typical car rounds it at a 50m radius and a speed of 13.4 m/s.

 

[PhanthomJay]

I think your suppose to find the angle. How come part b) is incorrect? I just plugged all the given numbers into find theta.


Here is b) Find the angle at which the curve should be banked if a typical car rounds it at a 50m radius and a speed of 13.4 m/s.

The tan of the angle is 0.366, not 0.366 radians. Now get out your calculator and find theta, and pay heed on the setting..is it degrees or radians or what??

 

[AznBoi]

The tan of the angle is 0.366, not 0.366 radians. Now get out your calculator and find theta, and pay heed on the setting..is it degrees or radians or what??

i don't get how you find the angle. I did the tan-1 on calculator using radian mode and I got .35125 radians. Is that the measurement of theta?

 

[PhanthomJay]

i don't get how you find the angle. I did the tan-1 on calculator using radian mode and I got .35125 radians. Is that the measurement of theta?

Sure you get it, your answer is correct. Theta = 0.35125 radians. Now put your calculator in degrees mode and you get 20.125 degerees, correct? Both answers are correct, they're just in different measures. Pi radians = 180 degrees, so one radian is about 57 degrees or so.

 

[AznBoi]

Sure you get it, your answer is correct. Theta = 0.35125 radians. Now put your calculator in degrees mode and you get 20.125 degerees, correct? Both answers are correct, they're just in different measures. Pi radians = 180 degrees, so one radian is about 57 degrees or so.

Oh ok! Thanks a lot for your help! So all of my steps for b) are correct then right? I don't know if I subsituted the correct numbers but I'm pretty sure I did. Thanks again!