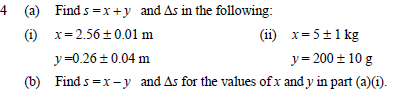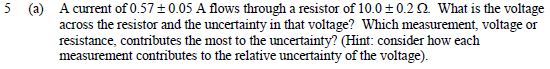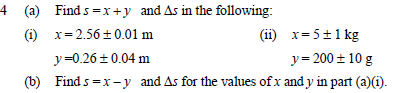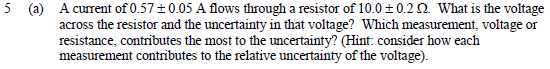- #1
TheFallen018
- 52
- 0
Hello,
I've been doing this quiz that is mostly based around uncertainties. I've got a few questions that I've got wrong, and was wondering if someone could give each a brief explanation. There's a few to go over, so if you'd be willing, I would be very grateful.
I've had a crack at these questions, but my understanding seems to be lacking. I could probably keep going on the questions until I get them right, but I don't feel like that would help my understanding much.
Here's the first question. Apparently two of these answers are correct.
View attachment 8292
Here is question two. Two of these are wrong. I think that part b and c need to be swapped, but I'm not clear on why.
View attachment 8293
View attachment 8294
The next part has one wrong. I can't tell where the error is, so my understanding of how uncertainties work is clearly missing something here.
View attachment 8295
View attachment 8296
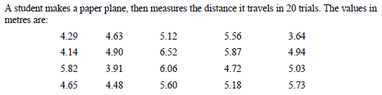
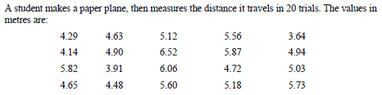
This one bothered me, because I can't see how some of the questions make sense, so some explanation on what I did wrong here would go a long way. I measured the standard deviation to be about 0.76, and the standard error in the mean to be about 0.17. The first question seemed strange because with just those measurements the standard deviation was already well below 1m. There are 2 wrong here.
View attachment 8297
View attachment 8298
Sorry for all of these questions. I really appreciate the time you've taken to read this far.
Thank-you. :)
I've been doing this quiz that is mostly based around uncertainties. I've got a few questions that I've got wrong, and was wondering if someone could give each a brief explanation. There's a few to go over, so if you'd be willing, I would be very grateful.
I've had a crack at these questions, but my understanding seems to be lacking. I could probably keep going on the questions until I get them right, but I don't feel like that would help my understanding much.
Here's the first question. Apparently two of these answers are correct.
View attachment 8292
Here is question two. Two of these are wrong. I think that part b and c need to be swapped, but I'm not clear on why.
View attachment 8293
View attachment 8294
The next part has one wrong. I can't tell where the error is, so my understanding of how uncertainties work is clearly missing something here.
View attachment 8295
View attachment 8296
This one bothered me, because I can't see how some of the questions make sense, so some explanation on what I did wrong here would go a long way. I measured the standard deviation to be about 0.76, and the standard error in the mean to be about 0.17. The first question seemed strange because with just those measurements the standard deviation was already well below 1m. There are 2 wrong here.
View attachment 8297
View attachment 8298
Sorry for all of these questions. I really appreciate the time you've taken to read this far.
Thank-you. :)