Solvng the Mass of an Object with a Vibrating String

In summary, the conversation discusses the determination of the mass of an object in a specific arrangement involving a string, pulley, and vibrator. The tension in the string is found to be equivalent to the weight of the mass, and the force cannot be divided into two halves. The participants express gratitude for the helpful insights provided by the conversation.
  • #1
new324
30
0
Once, again I find myself in need of a little help. Any hints/tips would be well appreciated.
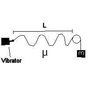
In the arrangement shown in (attachment), a mass m can be hund from a string (with a linear mass density of .002 kg/m) that passes over an ideal pulley. A string with a length of L=2 meters is connected to a vibrator of constant frequency, Find the mass m of the object when the standing waves with a fundamental frequency of 20 Hz are observed in the string.

Update: Alright I substitued a few equations and have determined the Tension. My assumption is that the mg is going to be half of the tension (half is mg the other half is the wave). Is this assumption correct? If not, any hints?
 

Attachments

  • example1.jpg
    example1.jpg
    3.2 KB · Views: 375
Last edited:
Physics news on Phys.org
  • #2
new324 said:
Update: Alright I substitued a few equations and have determined the Tension. My assumption is that the mg is going to be half of the tension (half is mg the other half is the wave). Is this assumption correct?
Think about it: The tension in the string must support the weight of the mass. Right?
 
  • #3
No, it's tension=m*g. Look at the situation without a wave: At the end of the string you'll have to pull with a force of m*g to prevent the mass from falling; hence the tension in the whole spring is m*g. If you run the oscillator now (with an arbitrarily small amplitude), this won't change, force can't be "splitted up" into two halfs in the same string.

Bruno
 
  • #4
Awesome. You guys are such a huge help to me. I always try and make things tougher than they are. Thank You!
 

FAQ: Solvng the Mass of an Object with a Vibrating String

1. How does a vibrating string help in solving the mass of an object?

When a string is attached to an object and is vibrated, it creates a standing wave pattern. The frequency of this wave is directly proportional to the mass of the object. By measuring the frequency and knowing the properties of the string, we can solve for the mass of the object using mathematical equations.

2. What is the relationship between the frequency and mass of an object in a vibrating string experiment?

The frequency of the standing wave on the string is inversely proportional to the mass of the object. This means that as the mass of the object increases, the frequency of the wave decreases. This relationship is described by the equation f = 1/2L√(T/m), where L is the length of the string, T is the tension, and m is the mass of the object.

3. What factors can affect the accuracy of the mass measurement in a vibrating string experiment?

There are several factors that can affect the accuracy of the mass measurement, including the tension and length of the string, the amplitude of the vibration, and the temperature of the environment. It is important to control these variables as much as possible to obtain an accurate measurement.

4. Can the vibrating string method be used to measure the mass of any object?

The vibrating string method can be used to measure the mass of small, compact objects that can be attached to the string and produce a standing wave. It is not suitable for measuring the mass of large or irregularly shaped objects, as the vibration may not produce a clear standing wave pattern.

5. Are there any alternative methods for solving the mass of an object besides using a vibrating string?

Yes, there are other methods for solving the mass of an object, such as using a balance or scale. However, the vibrating string method can be a useful alternative when a balance or scale is not available, or when measuring the mass of very small objects. It also offers a hands-on and visual approach to solving mass, making it a popular method in science experiments.

Similar threads

Waves and vibrations on a string
Replies
2
Views
1K
Finding the frequency of a string based on Mass and Tension
Replies
1
Views
2K
Mass atop four springs with external input: Reduce vibration amplitude by factor of ten
Replies
3
Views
373
Calculating Mass of a Vibrating String Using Known Quantities
Replies
10
Views
2K
Which Frequency is NOT Possible for a Vibrating String?
Replies
5
Views
1K
What will the wave velocity be in this string?
Replies
15
Views
2K
Tension Force between two rotating masses on strings
Replies
1
Views
3K
Tension in 4 strings suspending object at 4 different points
Replies
19
Views
4K
Eigenvalues of a string with fixed ends and a mass in the middle
Replies
2
Views
2K
A String is Connected to a Vibrating Arm and Passes Over a Light Pulley
Replies
2
Views
2K

Hot Threads

Recent Insights

Back
Top