Sound wave spreading radially question

[nophun6]

I have a question dealing with sound waves.

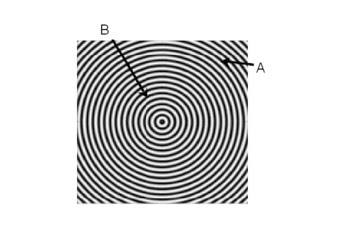
This figure shows waves spreading radially outward from a coherent source located at the center. The center spot represents a coherent source emitting at a constant frequency. Black indicates maxima (positive peaks) and white indicating minima (negative troughs)
a) The source is a speaker emitting a pure tone. Quantitatively speaking, would you hear a different sound intensity at points A and
B?
b) Is the quality of the sound (the tone) dependent
on location? That is, would you expect a
qualitatively different sound at different
locations?

I remember that the intenesity of sound decreases as sound increases because as the wave spreads further from the source to the areas of low and high pressure respecitively gain and lose pressure (compressions and rarefactions)
So would this mean that the sound you hear at point B is more intense than the sound you hear at point A?
And thus the quality of the sound is dependant on location?

thanks for the help;

 

[Chi Meson]

A) correct. Since the energy of the wave is spread out over the surface of an ever-increasing sphere, the intensity drops off as an inverse-square proportion with distance from source.

B) No. "Quality" is referring to what combination of frequencies you are hearing. This is a pure tone, and the frequency does not change as a function of distance from source.

 

[nophun6]

Ah, I see, thank you for your help. I have another question...

This picture depicts 2-source interference. There are 2 coherent sources emitting at the same frequency. Black indicates maxima, white indicates minima and pure gray corresponds to total destructive interference. Rank locations A-D according the intensities that a listener at each
location would experience (loudest to quietest).

So, in order from most intense to least: D(most intense) > C > A > B

I reasoned this from the fact that D is the closest and lies on a black line (maxima) and B, although not the furthest, lies in a grey region which means there is destructive interference.
Is this correct?
Thanks for the help!

 

[berkeman]

Yes, that's correct. Cool diagrams, BTW.