- #1
sander2798
- 8
- 0
Hello everyone,
I am trying to find out how space elevators work, but there is one think I can't figure out.
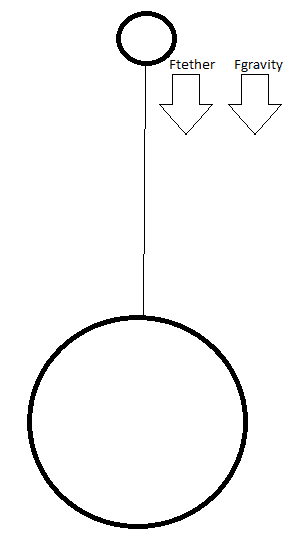
Normally, the forces on the countermass and it's tether will be as following, assuming you neglect the gravity on the tether.
But now, I put the lift somewhere on the cable (below geostationary orbit), like this.
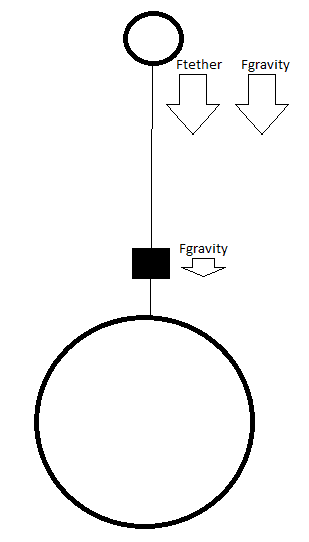
The total forces added up are more than the centripetal force needed to keep the counter mass in orbit, right? So how is it that the countermass doesn't come falling down?
Thanks in advance,
Sander.
I am trying to find out how space elevators work, but there is one think I can't figure out.
Normally, the forces on the countermass and it's tether will be as following, assuming you neglect the gravity on the tether.
But now, I put the lift somewhere on the cable (below geostationary orbit), like this.
The total forces added up are more than the centripetal force needed to keep the counter mass in orbit, right? So how is it that the countermass doesn't come falling down?
Thanks in advance,
Sander.