tigerseye
- 16
- 0
I've been stuck on this problem forever and I don't know how to do it if you can't use r as the radius.
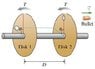
A bullet is shot through two cardboard disks attached a distance D apart to a shaft turning with a rotational period T (see the attached picture). Derive a formula for the bullet speed v in terms of D, T, and a measured angle theta between the position of the hole in the first disk and that of the hole in the second.
A bullet is shot through two cardboard disks attached a distance D apart to a shaft turning with a rotational period T (see the attached picture). Derive a formula for the bullet speed v in terms of D, T, and a measured angle theta between the position of the hole in the first disk and that of the hole in the second.