zasvitim
- 44
- 0
- TL;DR
- What will be the speed of reflected light?
Hello
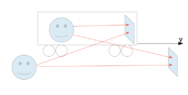
Let's suppose we have 2 observers. One is in Einstein's train and one is outside. There are 2 mirrors: one inside the train and one outside. Speed of train is v
Both observers emit light which reflects from both mirrors.
What will be the speed of reflected light for both observers from both mirrors? Will speeds be equal? Will there be 2 speeds? 4 speeds?
Thanks.
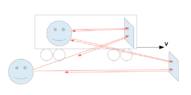
Let's suppose we have 2 observers. One is in Einstein's train and one is outside. There are 2 mirrors: one inside the train and one outside. Speed of train is v
Both observers emit light which reflects from both mirrors.
What will be the speed of reflected light for both observers from both mirrors? Will speeds be equal? Will there be 2 speeds? 4 speeds?
Thanks.