Karl86
- 40
- 3
Homework Statement
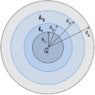
Consider the following system:
which consists of a conducting sphere with free charge , a dielectric shell with permittivity ##\epsilon_1##, another dielectric shell with permittivity ##\epsilon_2## and finally a conducting spherical shell with no free charge.
Homework Equations
##D = \epsilon_0 E+P##
##\sigma_b=P \cdot \hat{n}##
The Attempt at a Solution
After finding ##D=\frac{Q}{4\pi r^2}\hat{r}##, I calculated the polarization vector ##P_1,P_2## on each region to be
$$P_1=\left(1-\frac{\epsilon_0}{\epsilon_1}\right)\frac{Q}{4\pi r^2}\hat{r} \\
P_2=\left(1-\frac{\epsilon_0}{\epsilon_2}\right)\frac{Q}{4\pi r^2}\hat{r} $$
and the surface charge due to bound charges to be
$$ \sigma_{b_1}=\begin{cases}\frac{\epsilon_0 \chi_1 Q}{4\pi \epsilon_1 R_2^2} & \text{on outer surface} \\ -\frac{\epsilon_0 \chi_1 Q}{4\pi \epsilon_1 R_1^2} & \text{on inner surface} \end{cases}$$
$$ \sigma_{b_2}=\begin{cases}\frac{\epsilon_0 \chi_2 Q}{4\pi \epsilon_2 R_3^2}\hat{r} & \text{on outer surface} \\
-\frac{\epsilon_0 \chi_2 Q}{4\pi \epsilon_2 R_2^2}\hat{r} & \text{on inner surface} \end{cases}$$
##\rho_b=0## for both dielectrics because the divergence of ##P_i## is zero. Now I want to see that the overall induced charge is zero. I try to do this by integrating the surface distributions on each sphere and I get that the total charge induced by the dielectric 1 is ##\frac{\epsilon_0 \chi_1 Q}{\epsilon_1}## at ##R_2##, ##-\frac{\epsilon_0 \chi_1 Q}{\epsilon_1}## at ##R_1## and for the dielectric 2 it's ##\frac{\epsilon_0 \chi_2 Q}{\epsilon_2}## at ##R_3##, ##-\frac{\epsilon_0 \chi_2 Q}{\epsilon_2}## at ##R_2##. This seems to add up to zero, but I wonder whether these are the only induced charges in this setup or I'm forgetting something. Also: is integrating like that just the right way to compute the induced charge?
Thanks if you'll find time to help me somehow.