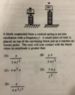Spring and Rock Homework: Finding Separation

  • Thread starter Thread starter Fontseeker
  • Start date Start date
  • Tags Tags
    Rock Spring
Click For Summary

Homework Help Overview

The discussion revolves around a problem involving a spring and a rock, focusing on the conditions under which the rock separates from the spring during oscillation. The subject area includes concepts from mechanics, specifically relating to forces, acceleration, and simple harmonic motion.

Discussion Character

  • Mixed

Approaches and Questions Raised

  • Participants explore the relationship between gravitational acceleration and the acceleration provided by the spring, questioning when the rock will separate from the spring. There are discussions about the conditions under which the spring's acceleration is greater or less than gravitational acceleration.

Discussion Status

The conversation is ongoing, with participants providing insights and questioning each other's reasoning. Some guidance has been offered regarding the relationship between acceleration and separation, but there is no clear consensus on the specific conditions or calculations needed to determine the amplitude at which separation occurs.

Contextual Notes

Participants are navigating through the implications of acceleration in the context of simple harmonic motion, with references to specific equations and the need to consider the signs of accelerations. There is an emphasis on understanding the relationship between amplitude and acceleration without reaching a definitive conclusion.

Fontseeker
Messages
30
Reaction score
4

Homework Statement



tnrkrkS7.jpg


Homework Equations



U = (1/2)kx^2
T = 2 * π * (m/k)^ (1/2)

The Attempt at a Solution


[/B]
T = 2 * π * (m/k)^ (1/2)
T ^ 2 = 4 * π^2 * (m/k)
k = (4 * π^2 * m) / T^2

So I know the initial potential energy is:

U = (1/2)kx^2
U = (1/2)x^2 * ((4 * π^2 * m) / T^2)

However, I don't know how to find where the rock and the spring separate?
 

Attachments

  • tnrkrkS7.jpg
    tnrkrkS7.jpg
    11.5 KB · Views: 856
Physics news on Phys.org
Fontseeker said:

Homework Statement



View attachment 225095

Homework Equations



U = (1/2)kx^2
T = 2 * π * (m/k)^ (1/2)

The Attempt at a Solution


[/B]
T = 2 * π * (m/k)^ (1/2)
T ^ 2 = 4 * π^2 * (m/k)
k = (4 * π^2 * m) / T^2

So I know the initial potential energy is:

U = (1/2)kx^2
U = (1/2)x^2 * ((4 * π^2 * m) / T^2)

However, I don't know how to find where the rock and the spring separate?
There is a constant force of gravity acting on the rock. When happens when the acceleration of gravity is greater than the acceleration provided by the spring? What happens when it is less?
 
tnich said:
There is a constant force of gravity acting on the rock. When happens when the acceleration of gravity is greater than the acceleration provided by the spring? What happens when it is less?
When the acceleration of gravity is greater than the spring, then they separate right?
 
Fontseeker said:
When the acceleration of gravity is greater than the spring, then they separate right?
You are close, but that's not quite it. Will the rock separate when it is traveling downward, or upward?
 
tnich said:
You are close, but that's not quite it. Will the rock separate when it is traveling downward, or upward?
The rock will separate as it is traveling upward, as soon as the spring stretches out (reaches its max amplitude), right?
 
Fontseeker said:
The rock will separate as it is traveling upward, as soon as the spring stretches out (reaches its max amplitude), right?
Nope. Your were closer before. The separation point has to do with the acceleration.
 
tnich said:
Nope. Your were closer before. The separation point has to do with the acceleration.
The spring will be acceleration up, and as long as the acceleration of the spring is greater than g, then so will the rock. As soon as the acceleration of the spring is less than g, it will separate right?
 
Fontseeker said:
The spring will be acceleration up, and as long as the acceleration of the spring is greater than g, then so will the rock. As soon as the acceleration of the spring is less than g, it will separate right?
Right in a sense. You need to think about the signs of the accelerations.
 
tnich said:
Right.
Now, I would just have to find the x at which the accelerations of both the spring and the rock equal the same using Newton's second law right?
 
  • #10
Fontseeker said:
Now, I would just have to find the x at which the accelerations of both the spring and the rock equal the same using Newton's second law right?
You were quick. I edited my answer. You still don't have it quite right. When the spring is accelerating upward and gravity is accelerating downward, the rock stay in contact. When the spring starts accelerating downward and it's acceleration downward is greater than the acceleration of gravity, then the rock will separate.
The question wants to know the amplitude at which the rock will separate. What equations do you know about simple harmonic motion that have acceleration and amplitude in them?
 
  • #11
tnich said:
You were quick. I edited my answer. You still don't have it quite right. When the spring is accelerating upward and gravity is accelerating downward, the rock stay in contact. When the spring starts accelerating downward and it's acceleration downward is greater than the acceleration of gravity, then the rock will separate.
The question wants to know the amplitude at which the rock will separate. What equations do you know about simple harmonic motion that have acceleration and amplitude in them?
I know a(t) = -Aw^2 * sin(wt). Now, I am trying to find when the acceleration starts accelerating downward, so I can just set to 0 right?
 
  • #12
Fontseeker said:
I know a(t) = -Aw^2 * sin(wt). Now, I am trying to find when the acceleration starts accelerating downward, so I can just set to 0 right?
If you were holding a rock stationary on the palm of your hand, how fast would you have to accelerate your hand downward so that rock would fall freely?
 
  • #13
jbriggs444 said:
If you were holding a rock stationary in your hand, how fast would you have to accelerate your hand downward so that rock would fall freely?
I would have to accelerate it down at g.
 
  • #14
Fontseeker said:
I would have to accelerate it down at g.
Right! So how fast does the block on which the fragment is resting have to accelerate downward so that the fragment falls free?
 
  • #15
jbriggs444 said:
Right! So how fast does the block on which the fragment is resting have to accelerate downward so that the fragment falls free?
I am not really understanding your question
 
  • #16
Fontseeker said:
I am not really understanding your question
Replace your palm with a block. How fast does the block have to accelerate downward so that a rock sitting on top falls free?
 
  • #17
jbriggs444 said:
Replace your palm with a block. How fast does the block have to accelerate downward so that a rock sitting on top falls free?
It has to accelerate down at 9.8m/s^2
 
  • #18
Fontseeker said:
It has to accelerate down at 9.8m/s^2
Right! Now all you have to do is figure out what amplitude of an oscillation results in the block having a downward 9.8 m/s^2 acceleration at some point.
 
  • #19
jbriggs444 said:
Right! Now all you have to do is figure out what amplitude of an oscillation results in the block having a downward 9.8 m/s^2 acceleration at some point.

I could use this equation, but I don't know w: a(t) = -Aw^2 * sin(wt)
 
  • #20
Fontseeker said:
I could use this equation, but I don't know w: a(t) = -Aw^2 * sin(wt)
You know that the maximum downward acceleration occurs when sin(ωt) = what?

Edit: and you do know ω -- it is a function of f.
 
  • #21
jbriggs444 said:
You know that the maximum downward acceleration occurs when sin(ωt) = what?

Edit: and you do know ω -- it is a function of f.
sin(wt) = g / (Aw^2) right?

Would you find w using conservation of energy or how would you find it?
 
  • #22
Write omega in terms of f. The multiple choice answers you are given use f.

Edit: Also, answer the question: For a given amplitude A, the maximum downward acceleration of the block occurs when sin(ωt) = what?
 
  • #23
jbriggs444 said:
Write omega in terms of f. The multiple choice answers you are given use f.

Edit: Also, answer the question: For a given amplitude A, the maximum downward acceleration of the block occurs when sin(ωt) = what?

sin(wt) = g / (Aw^2) and then replace w using frequency right?
 
  • #24
Fontseeker said:
sin(wt) = g / (Aw^2) and then replace w using frequency right?
Way easier than that.

The acceleration is maximum when sin(ωt) is maximum. What is the maximum value of sin(ωt)?
 

Similar threads

Finding Spring Constant & Energy w/ Doubt in Exercise
  • · Replies 7 ·
Replies
7
Views
2K
Spring Problem Involving Variables and Constants Only
  • · Replies 3 ·
Replies
3
Views
2K
Speed of a pendulum at the bottom
  • · Replies 4 ·
Replies
4
Views
4K
Position and acceleration in simple harmonic motion given velocity
  • · Replies 16 ·
Replies
16
Views
2K
Energy stored in a double spring system
  • · Replies 17 ·
Replies
17
Views
2K
Determine expressions for the following in terms of M, X, D, h and g
  • · Replies 30 ·
2
Replies
30
Views
2K
Mass atop four springs with external input: Reduce vibration amplitude by factor of ten
  • · Replies 3 ·
Replies
3
Views
1K
What is the Relationship Between Force and Spring Constant?
  • · Replies 14 ·
Replies
14
Views
4K
What Is the Connection Between Buoyancy and Apparent Mass?
  • · Replies 2 ·
Replies
2
Views
2K
Finding a formula for displacement of a mass on a spring using v.
  • · Replies 2 ·
Replies
2
Views
867