Spring force and the force of friction

[curicuri]

Homework Statement

A box with a mass of 20 kg is put on a vertical table that is is free from friction. On top of that box is another box with the mass of 2 kg. The friction number between the boxes are 0,35. The big box that lays on the table has a spring attached to it, that has the "spring-constant"=400N/m. The spring is attached to the wall on the other end.
Determine max amplitude that can be obtained without the small box falling off.

Relevant Equations

Ff=Fr

Hello, do someone have time to help me out with an assignment?

My question
In the answer sheet they say:

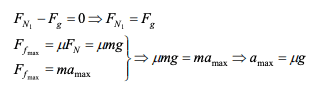
What I do not understand is why m is withdrawn from both sides, since I don't see that those represent the same mass. When I did the assignment I thought m at the left side would be the mass of the small box, and m at the right side would be the mass of the big box. That was why I did not cancel m out, which was why I got the wrong answer.

 

[RPinPA]

You want to know that the friction between the boxes is large enough to accelerate the small box with the same acceleration. So $m$ is the small box on both sides.

 

[curicuri]

AA of course, thank you :)